计算机图形学课件-fifth.ppt

《计算机图形学课件-fifth.ppt》由会员分享，可在线阅读，更多相关《计算机图形学课件-fifth.ppt（38页珍藏版）》请在三一办公上搜索。

1、2023/8/25,计算机图形学演示稿 纪玉波制作(C),1,第五章 图形变换,在计算机绘图应用中，经常要进行从一个几何图形到另一个几何图形的变换，例如，将图形向某一方向平移一段距离；将图形旋转一定的角度；或将图形放大或缩小等等，这种变换过程称为几何变换。图形的几何变换是计算机绘图中极为重要的一个组成部分，利用图形变换还可以实现二维图形和三维图形之间转换，甚至还可以把静态图形变为动态图形，从而实现景物画面的动态显示。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),2,5.1 二维图形变换 二维图形几何变换的基本原理 二维平面图形的几何变换是指在不改变图形连线次序的情况下，对一个平面

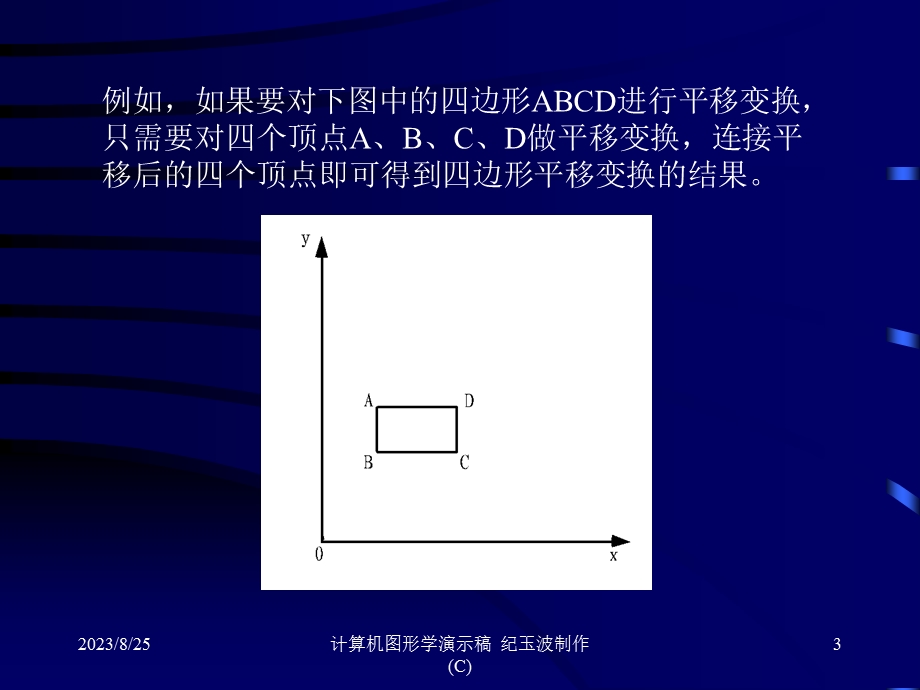
2、点集进行的线性变换。实际上，由于一个二维图形可以分解成点、直线、曲线。把曲线离散化，它可以用一串短直线段来逼近，而每一条直线段均由两点所决定，这样，二维平面图形不论是由直线段组成，还是由曲线段组成，都可以用它的轮廓线上顺序排列的平面点集来描述。因此可以说，对图形作几何变换，其实质是对点的几何变换，通过讨论点的几何变换，就可以理解图形几何变换的原理。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),3,例如，如果要对下图中的四边形ABCD进行平移变换，只需要对四个顶点A、B、C、D做平移变换，连接平移后的四个顶点即可得到四边形平移变换的结果。,2023/8/25,计算机图形学演示稿 纪

3、玉波制作(C),4,对二维图形进行几何变换有五种基本变换形式，它们是：平移、旋转、比例、对称和错切，这些图形变换的规则可以用函数来表示。有两种不同的变换形式：一种是图形不动，而坐标系变动，即变换前与变换后的图形是针对不同坐标而言的，称之为坐标模式变换；另一种是坐标系不动，而图形改变，即变换前与变换后的坐标值是针对同一坐标系而言的，称之为图形模式变换。实际应用中，后一种图形变换更有实际意义，下面讨论的图形变换是属于后一种变换。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),5,平移变换 平移变换是指将图形从一个坐标位置移到另一个坐标位置的重定位变换。已知一点的原始坐标是P(x,y），

4、加上一个沿X，Y方向的平移量tx 和ty，平移此点到新坐标（xtx,yty）,则新坐标的表达式为：,如果对一图形的每个点都进行上述变换，即可得到该图形的平移变换。实际上，线段是通过对其两端点进行平移变换，多边形的平移是平移每个顶点的坐标位置，曲线可以通过平移定义曲线的坐标点位置，用平移过的坐标点重构曲线路径来实现。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),6,平移变换只改变图形的位置，不改变图形的大小和形状。下图是一平移变换的例子。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),7,可以用矩阵形式来表示二维平移变换方程。图形变换通常使用齐次坐标矩阵来表示。平移变换

5、方程的齐次坐标矩阵表示式为：,其中,称为变换矩阵。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),8,有了上面的矩阵表示，连续的平移变换可以通过连续的矩阵乘法来实现。例如,点经平移变换T1（tx1,ty1）后，再经平移变换T2（tx2,ty2），那么，最终的平移变换矩阵。5.1.3 比例变换 一个图形中的坐标点P(x,y）若在X轴方向变化一个比例系数sx，在Y轴方向变化一个比例系数sy，则新坐标点P(x,y）的表达式为：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),9,这一变换称为相对于坐标原点的比例变换,sx 和sy分别表示点P(x,y）沿X轴方向和Y轴方向相对坐标

6、原点的比例变换系数。比例变换改变图形的大小。变换方程写成齐次坐标矩阵形式为：,其中变换矩阵：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),10,比例变换系数sx和sy可赋予任何正数值。当值小于1时缩小图形，值大于1则放大图形。当sx和sy被赋予相同值时，就产生保持图形相对比例一致的变换,sx和sy值不等时产生X轴方向和Y轴方向大小不等的比例变换。sx和sy都指定为1时，图形大小不改变。实际上，相对于坐标原点图形的比例变换，相当于每一点相对于坐标原点的变换，因此，它不但改变图形的大小，而且改变图形的位置。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),11,下图是一图形

7、比例变换的例子：,中心在原点的放大变换,中心不在原点的放大变换,2023/8/25,计算机图形学演示稿 纪玉波制作(C),12,可以通过选择一个在变换后不改变位置的固定点Pc(xc,yc),来控制图形变换的位置。例对于多边形图形，固定点的坐标(xc,yc)可以选择图形的某个顶点、图形几何中心点或任何其它位置，这样变换后固定点坐标不改变，多边形每个顶点相对于固定点缩放。对于坐标为P(x,y)的顶点，相对于固定点Pc(xc,yc)变换后的坐标P(x,y)可计算为：,写成齐次坐标矩阵形式为：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),13,其中变换矩阵：,计算公式的推导可以这样考虑，

8、先平移坐标原点（0,0）到（xc,yc），然后进行比例变换，变换后再将坐标原点移回到（0,0）。三个过程的结果就是相对于点（xc,yc）的比例变换。三个过程的变换矩阵分别是：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),14,2023/8/25,计算机图形学演示稿 纪玉波制作(C),15,5.1.4 旋转变换 若图形中的坐标点P(x,y)绕坐标原点逆时针旋转一个角度,则新坐标点P(x,y）的表达式为：,公式的推导可参考右图,2023/8/25,计算机图形学演示稿 纪玉波制作(C),16,变换方程写成齐次坐标矩阵形式为：,其中变换矩阵,上面是点P(x,y)以坐标原点为中心的旋转变换

9、，还可以任意点Pc(xc,yc）为中心做旋转变换。其变换公式为：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),17,此公式的推导过程可以这样考虑，先平移坐标原点（0,0）到（xc,yc），然后进行旋转变换，变换后再将坐标原点移回到（0,0）。三个过程的结果就是以点（xc,yc）为中心的旋转变换。写成齐次坐标矩阵形式为：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),18,其中变换矩阵:,旋转变换只能改变图形的方位，而图形的大小和形状不变。旋转变换的几何表示见下图。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),19,5.1.5 对称变换 对称变换是产生图形

10、镜象的一种变换，也称镜象变换或反射变换。将图形绕对称轴旋转就可以生成镜象图形。1.对称于X轴 当变换对称于X轴时，则坐标点P(x,y)经对称变换后，新坐标点P(x,y）的表达式为：,变换方程写成齐次坐标矩阵形式为：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),20,其中变换矩阵：,对称X轴变换的几何表示见下图,2023/8/25,计算机图形学演示稿 纪玉波制作(C),21,2.对称于Y轴 当变换对称于Y轴时，则坐标点P(x,y)经对称变换后，新坐标点P(x,y）的表达式为：,变换方程写成齐次坐标矩阵形式为：,其中变换矩阵：,2023/8/25,计算机图形学演示稿 纪玉波制作(C)

11、,22,对称Y轴变换的几何表示见下图,2023/8/25,计算机图形学演示稿 纪玉波制作(C),23,3.对称于原点 当图形对X轴和Y轴都进行对称变换时，即得相对于坐标原点的对称变换。这一变换前后点坐标之间的关系为：,写成齐次坐标矩阵形式为：,其中变换矩阵：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),24,对称原点变换的几何表示见下图,2023/8/25,计算机图形学演示稿 纪玉波制作(C),25,4.对称平行于X轴的直线 当对称轴是平行于X轴的直线yyc时，变换前后点的坐标之间的关系为：,变换方程写成齐次坐标矩阵形式为：,其中变换矩阵：,2023/8/25,计算机图形学演示稿

12、 纪玉波制作(C),26,5.对称平行于Y轴的直线 当对称轴是平行于Y轴的直线xxc时，变换前后点的坐标之间的关系为：,变换方程写成齐次坐标矩阵形式为：,其中变换矩阵：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),27,6.对称于任一点(xc,yc)的变换 对称于任一点(xc,yc)的变换，实际上可以看做分别相对于直线轴xxc和直线轴 yyc的两次对称变换，因此其变换公式是两者的综合：,变换方程写成齐次坐标矩阵形式为：,其中变换矩阵：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),28,7对称于任一轴的变换 关于XY平面内任一直线ymxb为对称轴的变换，可以分解为平移

13、、旋转、对称于坐标轴等变换的组合。首先平移直线经过坐标原点，而后将直线绕坐标原点旋转至同某一坐标轴重合，做对称于坐标轴的变换，最后反向旋转和反向平移将直线置回原处。如下图所示，平移直线经过坐标原点需要在Y轴方向上移动距离b，然后将直线绕坐标原点旋转至同Y轴重合，设旋转角度为，两步的变换矩阵分别为：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),29,做对称于Y轴的对称变换，其变换矩阵为：,最后反向旋转和反向平移将直线置回原处，其变换矩阵分别为：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),30,所以，对称于任一轴ymxb的变换矩阵为：,变换矩阵中的和需要用已知量表示出

14、来。当m为直线斜率，b为截距时有：,所以,2023/8/25,计算机图形学演示稿 纪玉波制作(C),31,替换变换矩阵中的和得：,上述变换用代数方程表示为：,2023/8/25,计算机图形学演示稿 纪玉波制作(C),32,5.1.6 错切变换 错切（shear）变换是轴上点不动，其它点沿平行于此轴方向移动变形的变换。错切变换也称为剪切、错位或错移变换。常用的错切变换有两种：改变x坐标值和改变y坐标值。,1.沿X轴方向关于Y的错切 变换前和变换后y坐标不变，而x坐标根据y坐标值呈线性变化。变换前后点的坐标之间的关系为：,式中c为错切系数。若c0，则沿+X方向错切，若c0，则沿-X方向错切。,20

15、23/8/25,计算机图形学演示稿 纪玉波制作(C),33,下图说明了矩形ABCD经错切变换后变为ABCD的结果。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),34,变换方程写成齐次坐标矩阵形式为：,其中变换矩阵:,2023/8/25,计算机图形学演示稿 纪玉波制作(C),35,2.沿Y轴方向关于X的错切 变换前和变换后x坐标不变，而y坐标根据x坐标值呈线性变化。变换前后点的坐标之间的关系为：,式中d为错切系数。若d0，则沿+Y方向错切，若d0，则沿-Y方向错切。右图说明了矩形ABCD经错切变换后结果为ABCD。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),36,变

16、换方程写成齐次坐标矩阵形式为：,其中变换矩阵:,除了沿X轴方向和沿Y轴方向的错切变换外，还可以使用沿平行于X轴方向的轴线或沿平行于Y轴方向的轴线以及任一轴线的错切变换。对于这些变换，可以通过先平移、旋转轴线，转化为沿X轴方向或沿Y轴方向的错切变换。错切变换不仅改变图形的形状，而且改变图形的方位，还可能使图形发生畸变。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),37,上面讨论的五种变换给出的都是点变换的公式，图形的变换实际上都可以通过点变换完成。例如直线段的变换可通过变换两个端点，并重画新端点间的线而得到。多边形的变换可通过变换每个顶点，并用新的顶点来生成多边形而实现。曲线的变换

17、可通过变换控制点并重画线来完成。符合下面形式：,的坐标变换称为二维仿射变换（Affine Transformation）。变换的坐标x和y都是原始坐标x和y的线性函数。参数aij是由变换类型确定的常数。仿射变换具有平行线转换成平行线和有限点映射到有限点的一般特性。,2023/8/25,计算机图形学演示稿 纪玉波制作(C),38,平移、比例、旋转、对称和错切变换都是二维仿射变换的特例，任何常用的二维仿射变换总可表示为这五种变换的组合。平移、比例、旋转、对称的仿射变换保持变换前后两直线间的角度、平行关系和长度之比不改变。5.1.7 复合变换 所谓二维图形的复合变换，就是在XY平面内，对一个已定义的图形，按一定顺序进行多次变换而得到新的图形。一般把上面讨论的五种变换称为基本的图形变换，绝大部分复杂的图形变换都可以通过这些基本变换的适当组合来实现。利用前面所提供的矩阵表示，就可通过计算单个变换的矩阵乘积，将任意顺序变换的矩阵建立为复合变换矩阵。,