《牛顿迭代法》PPT课件.ppt

《《牛顿迭代法》PPT课件.ppt》由会员分享，可在线阅读，更多相关《《牛顿迭代法》PPT课件.ppt（40页珍藏版）》请在三一办公上搜索。

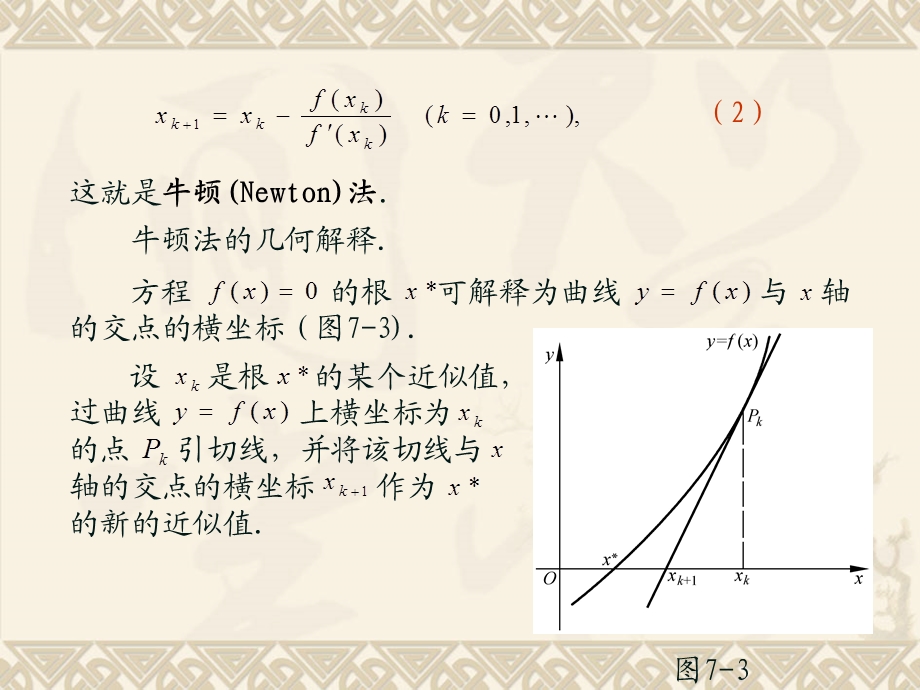
1、一 牛顿法及其收敛性,牛顿法是一种线性化方法，其基本思想是将非线性方程 逐步归结为某种线性方程来求解.,设已知方程 有近似根（假定)，将函数 在点 展开，有,于是方程 可近似地表示为,（1）,这是个线性方程，记其根为，则 的计算公式为,10.4 牛顿迭代法,（2）,这就是牛顿(Newton)法.,牛顿法的几何解释.,方程 的根 可解释为曲线 与 轴的交点的横坐标（图7-3).,设 是根 的某个近似值，过曲线 上横坐标为 的点 引切线，并将该切线与 轴的交点的横坐标 作为 的新的近似值.,图7-3,注意到切线方程为,这样求得的值 必满足(1），从而就是牛顿公式（2）的计算结果.由于这种几何背景，

2、牛顿法亦称切线法.,牛顿法（2）的收敛性，可直接由上节定理得到，对（2）其迭代函数为,由于,假定 是 的一个单根，即，则由上式知，于是依据可以断定，牛顿法在根 的邻近至少是平方收敛的.,又因,故 可得,（3.3）,例7.3.1 用牛顿法解方程,（3.4）,解 这里牛顿公式为,取迭代初值，迭代结果列于表7-5中.,所给方程（3.4）实际上是方程 的等价形式.若用不动点迭代到同一精度要迭代28次，可见牛顿法的收敛速度是很快的.,对于给定的正数，应用牛顿法解二次方程,可导出求开方值 的计算程序,（3.5）,这种迭代公式对于任意初值 都是收敛的.,事实上，对（3.5）式施行配方手续，易知,二 牛顿法应

3、用举例,以上两式相除得,据此反复递推有,（3.6）,记,整理（3.6）式，得,对任意，总有，故由上式推知，当 时，即迭代过程恒收敛.,解 取初值，对 按（3.5）式迭代3次便得到精度为 的结果（见表7-6).,由于公式（3.5）对任意初值 均收敛，并且收敛的速度很快，因此可取确定的初值如 编成通用程序.,例7.3.2 求.,三 简化牛顿法与牛顿下山法,牛顿法的优点 收敛快，牛顿法的缺点 一 每步迭代要计算 及，计算量较大且有时 计算较困难，二是初始近似 只在根 附近才能保证收敛，如 给的不合适可能不收敛.,为克服这两个缺点，通常可用下述方法.,（1）简化牛顿法，也称平行弦法.其迭代公式为,（3

4、.7）,迭代函数,若在根 附近成立，即取，则迭代法（3.7）局部收敛.,在（3.7）中取，则称为简化牛顿法，这类方法计算量省，但只有线性收敛，其几何意义是用平行弦与 轴交点作为 的近似.如图7-4所示.,图7-4,（2）牛顿下山法.,牛顿法收敛性依赖初值 的选取.如果 偏离所求根 较远，则牛顿法可能发散.,例如，用牛顿法求方程,（3.8）,在 附近的一个根.,设取迭代初值，用牛顿法公式,（3.9）,计算得,迭代3次得到的结果 有6位有效数字.,但如果改用 作为迭代初值，则依牛顿法公式（3.9）迭代一次得,这个结果反而比 更偏离了所求的根.,为了防止迭代发散，对迭代过程再附加一项要求，即具有单调

5、性：,（3.10）,满足这项要求的算法称下山法.,将牛顿法与下山法结合起来使用，即在下山法保证函数值稳定下降的前提下，用牛顿法加快收敛速度.,将牛顿法的计算结果,与前一步的近似值 适当加权平均作为新的改进值,（3.11）,其中 称为下山因子，（3.11）即为,（3.12）,(3.12)称为牛顿下山法.,选择下山因子时从 开始，逐次将 减半进行试算，直到能使下降条件（3.10）成立为止.,若用此法解方程（3.8），当 时由（3.9）求得,，它不满足条件（3.10）.,通过 逐次取半进行试算，当 时可求得.此时有，而显然.,由 计算 时,均能使条件（3.10）成立.计算结果如下：,即为 的近似.一

6、般情况只要能使条件（3.10）成立，则可得到，从而使 收敛.,四 重根情形,设，整数，则 为方程 的 重根，此时有,只要 仍可用牛顿法（3.2）计算，此时迭代函数,的导数为,且，所以牛顿法求重根只是线性收敛.,则.用迭代法,（3.13）,求 重根，则具有2阶收敛，但要知道 的重数.,构造求重根的迭代法，还可令，若 是 的 重根，则,若取,故 是 的单根.对 用牛顿法，其迭代函数为,从而可构造迭代法,（3.14）,它是二阶收敛的.,例7.3.3 方程 的根 是二重根，用上述三种方法求根.,解 先求出三种方法的迭代公式：,（1）牛顿法,（2）用（3.13）式,（3）用（3.14）式,取初值，计算结

7、果如表7-7.,计算三步，方法（2）及（3）均达到10位有效数字，而用牛顿法只有线性收敛，要达到同样精度需迭代30次.,五 弦截法与抛物线法,用牛顿法求方程（1.1）的根，每步除计算 外还要算，当函数 比较复杂时，计算 往往较困难，为此可以利用已求函数值 来回避导数值 的计算.,1 弦截法,设 是 的近似根，利用 构造一次插值多项式，并用 的根作为新的近似根.由于,（5.1）,因此有,（5.2）,（5.2）可以看做牛顿公式,中的导数 用差商 取代的结果.,几何意义.,曲线 上横坐标为 的点分别记为，则弦线 的斜率等于差商值,其方,程是,因之，按（5.2)式求得的 实际上是弦线 与 轴交点的横坐

8、标.这种算法因此而称为弦截法.,表7-5,弦截法与切线法（牛顿法）都是线性化方法，但两者有本质的区别.,切线法在计算 时只用到前一步的值，而弦截法（5.2），在求 时要用到前面两步的结果，因此使用这种方法必须先给出两个开始值.,例7.3.4 用弦截法解方程,解 设取 作为开始值，用弦截法求得的结果见表7-8，比较例7.3.1牛顿法的计算结果可以看出，弦截法的收敛速度也是相当快的.,实际上，弦截法具有超线性的收敛性.,定理6 假设 在根 的邻域 内具有二阶连续导数，且对任意 有，又初值，那么当邻域充分小时，弦截法（5.2）将按阶 收敛到根.这里 是方程 的正根.,2 抛物线法,设已知方程 的三个

9、近似根，以这三点为节点构造二次插值多项式，并适当选取 的一个零点 作为新的近似根，这样确定的迭代过程称抛物线法，亦称密勒（Mller）法.,在几何上，这种方法的基本思想是用抛物线 与 轴的交点 作为所求根 的近似位置（图7-6).,图7-6,插值多项式,有两个零点：,（5.3）,式中,问题是该如何确定，假定在 三个近似根中，更接近所求的根，为了保证精度，选（5.3）中较接近 的一个值作为新的近似根.为此，只要取根式前的符号与 的符号相同.,例7.3.5 用抛物线法求解方程,解 设用表7-8的前三个值,作为开始值，计算得,故,代入（5.3）式求得,以上计算表明，抛物线法比弦截法收敛得更快.,在一

10、定条件下可以证明，对于抛物线法，迭代误差有下列渐近关系式,可见抛物线法也是超线性收敛的，其收敛的阶,收敛速度比弦截法更接近于牛顿法.,从（5.3）看到，即使 均为实数，也可以是复数，所以抛物线法适用于求多项式的实根和复根.,7.6 解非线性方程组的牛顿迭代法,考虑方程组,（6.1）,其中 均为 的多元函数.,用向量记号记,(6.1）就可写成,（6.2）,当，且 中至少有一个是自变量,的非线性函数时，称方程组（6.1）为非线性方程组.,非线性方程组求根问题是前面介绍的方程（即）求根的直接推广，只要把前面介绍的单变量函数 看成向量函数 则可将单变量方程求根方法推广到方程组（6.2）.,若已给出方程（6.2）的一个近似根，将函数 的分量 在 用多元函数泰勒展开，并取其线性部分，则可表示为,令上式右端为零，得到线性方程组,（6.3）,其中,（6.4）,称为 的雅可比(Jacobi)矩阵.,求解线性方程组（6.3）并记解为，则得,（6.5）,这就是解非线性方程组（6.2）的牛顿迭代法.,例12 求解方程组,给定初值,用牛顿法求解.,解 先求雅可比矩阵,由牛顿法（6.5）得,即,由 逐次迭代得到,的每一位都是有效数字.,拟Newton方程,1.,其中,例1用拟newton法和Broyden秩1修改方法求,