第4章平面力系的简化课件.ppt

《第4章平面力系的简化课件.ppt》由会员分享，可在线阅读，更多相关《第4章平面力系的简化课件.ppt（78页珍藏版）》请在三一办公上搜索。

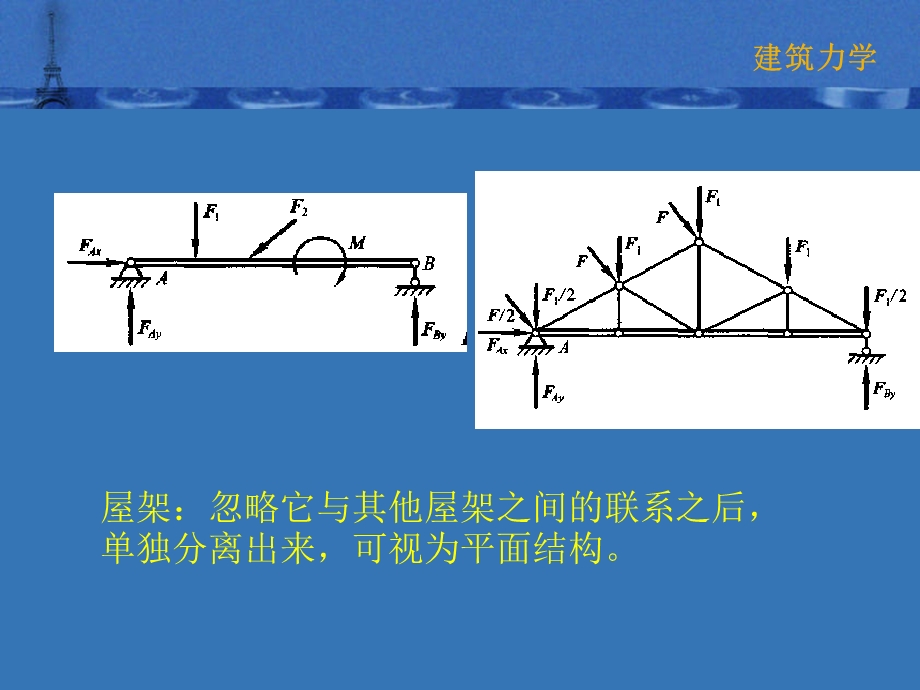
1、平面任意力系：力系中各力的作用线都在同一平面内，且任意分布。工程中的多数问题都简化为平面任意力系问题来解决。本意内容在工程实践中应用广泛。（1）当物体所受的力对称于某一平面时，可以简化为平面任意力系来处理。（2）有些结构所受的力系本不是平面任意力系，但可以简化为平面任意力系来处理。如屋架，在忽略它与其他屋架之间的联系之后，单独分离出来，可视为平面结构。,第 4章 平面力系的简化与平衡方程,屋架：忽略它与其他屋架之间的联系之后，单独分离出来，可视为平面结构。,力系向任意一点O 的简化,应用力的等效平移定理，将平面一般力系中的各个力（以三个力为例）全部平行移到作用面内某一给定点O。从而这力系被分解

2、为一个平面汇交力系和一个平面力偶系。这种等效变换的方法称为力系向给定点O 的简化。点O 称为简化中心。,第 4章 平面力系的简化与平衡方程,4-1 平面任意力系向一点的简化 主矢和主矩,汇交力系F1、F2、F3 的合成结果为一作用在点O 的力F R。这个力矢FR 称为原平面任意力系的主矢。F R=F1+F2+F3=Fi,附加力偶系的合成结果是一个作用在同一平面内的力偶 Mo，称为原平面任意力系对简化中心 O 的主矩。Mo=Mo(F1)+Mo(F2)+Mo(F3)=Mo(Fi),因此，平面任意力系向任意一点的简化结果为一个主矢FR 和一个主矩M，这个结果称为平面任意力系的一般简化结果。,第 4章

3、 平面力系的简化与平衡方程,一般情形，平面任意力系向作用面内任选一点O简化，可得一个力和一个力偶。此力等于该力系的主矢（力系中各力的矢量和），作用线通过简化中心O。此力偶的矩等于该力系对于点O的主矩（力系中各力对简化中心的矩的代数和）。,几点说明：1、一般情况下，平面任意力系等效于一力和一力偶。主矢一般不与原力系等效，不是原力系的合力；附加力偶系的合力偶M，一般不与原力系等效，不是原力系的合力偶。2、平面任意力系的主矢大小和方向与简化中心位置无关。主矢等于各力的矢量和，由力系中各力矢量和确定，故与主矢简化中心的选择无关。对于给定的力系，选取不同的简化中心，所得主矢相同。2、平面任意力系的主矩大

4、小和转向与简化中心O 位置有关。主矩等于各力对简化中心的矩的代数和，选取不同的点作为简化中心，各力的力臂将有改变，各力对简化中心的矩也有改变，所以，一般情况下，主矩与简化中心的选择位置有关。对于给定的力系，选取不同的简化中心，所得主矩一般不同。因此，在说到力系的主矩时，一定要指明是力系对于哪一点的主矩。,第 4章 平面力系的简化与平衡方程,第 4章 平面力系的简化与平衡方程,力系的主矢可以用解析的方法求得。力系的主矩可以直接用力系中各力对简化中心O之矩的代数和求出；,主矢的解析计算：,主矢，主矢方向角的正切可按力多边形规则作图求得或用解析法计算。,第 4章 平面力系的简化与平衡方程,式中Fxi

5、，Fyi是力Fi在x轴和y轴上的投影。,分别代表主矢FR与x和y轴正向的夹角。,教材符号订正：公式(4-3，5)FR撇号,主矩 Mo计算：,主矩的解析计算：,第 4章 平面力系的简化与平衡方程,其中xi，yi为力Fi作用点的坐标。,例 4.1 在边长为a1m的正方形的四个顶点上，作用有F1、F2、F3、F4等四个力。已知F140N，F260N，F360 N，F480 N。试求该力系向点A简化的结果。,第 4章 平面力系的简化与平衡方程,解：选坐标系。求力系主矢FR。,第 4章 平面力系的简化与平衡方程,为主矢与x和y轴正向夹角。可以用90进行校核。力系相对于简化中心A的主矩计算如下，负号表明力

6、偶为顺时针转向。,第 4章 平面力系的简化与平衡方程,应用力向一点简化的方法分析固定端支座的约束反力。固定端或插入端支座：一物体的一端完全固定在另一物体上，这种约束称为。如电线杆，外伸阳台，机加工刀具固定架，工件卡盘等。,固定端支座对物体的作用，是在接触面上作用了一群约束力。在平面问题中，这些力为一平面任意力系，如图b所示。,第 4章 平面力系的简化与平衡方程,将这群力向作用平面内的点A简化得到一个力FA和一个力偶MA。图c。一般情况下这个力的大小和方向均为未知量。可用两个未知分力来代替。因此，在平面力系情况下，固定端A处的约束作用力可简化为两个约束力FAx，FAy和一个矩为MA的约束力偶。,

7、第 4章 平面力系的简化与平衡方程,比较固定端支座与固定铰链支座的约束性质可见，固定端支座除了限制物体在水平方向和铅直方向移动外，还能限制物体在乎面内转动。因此，除了约束力FAx，FAy外，还有矩为MA的约束力偶。而固定铰链支座没有约束力偶，因为它不能限制物体在平面内的转动。,4-2 平面任意力系简化结果的讨论 平面任意力系向简化中心o简化，一般得一力和一力偶。可能出现的情况有四种：,1主矢不为零，主矩为零 附加力偶系的合力偶矩为零，原力系只与一个力等效，力系简化为一合力，此合力的矢量即为力系的主矢FR，合力作用线恰好通过简化中心o。,第 4章 平面力系的简化与平衡方程,2主矢、主矩均不为零

8、力系等效于一作用于简化中心o的力FR和一力偶矩为Mo的力偶。由力的平移定理知，一个力可以等效地变换成为一个力和一个力偶，那么，反过来，也可将一力和一力偶等效地变换成为一个力。即，当主矢和主矩均不为零时，可简化为一合力。合力FR与主矢FR具有相同的大小和方向。合力作用线不再通过简化中心o，而是位于主矢FR的一侧，使得合力FR对o点的矩与主矩Mo具有相同的正负号，且合力FR与主矢FR间的距离d可由下式确定：,第 4章 平面力系的简化与平衡方程,第 4章 平面力系的简化与平衡方程,平面任意力系合力矩定理证明,任选简化中心O，上式普遍成立。由此可得出前面学过的合力矩定理。平面任意力系的合力对作用面内任

9、意一点的矩等于力系中各力对同一点的矩的代数和。,Mo是该力系对于点O的主矩，等于力系中各力对简化中心O的矩的代数和。,由图易见，合力FR对点O的矩为,第 4章 平面力系的简化与平衡方程,例4.2 求例4.1中所给定的力系的合力作用线。在前面己求出力系向点A简化的结果，且主矢和主矩都不等于零。这说明力系可简化为一合力FR。且FR FR。,关键问题是要确定出合力FR的作用线在坐标系中的位置。即与x轴的交点K的坐标xK。,第 4章 平面力系的简化与平衡方程,设想将合力FR沿作用线移至K点，分解为两个分力FRx和FRy。力系向点A简化的主矩为MA，根据合力矩定理。,式中负号表明K点在坐标原点A的左侧。

10、,3主矢为零，主矩不为零各力向简化中心等效平移后，所得汇交力系是平衡力系，原力系与附加力偶系等效。原力系简化为一合力偶，该力偶的矩就是原力系相对于简化中心O的主矩Mo。此种情况下，主矩与简化中心的位置无关，向不同点简化，所得主矩相同。,第 4章 平面力系的简化与平衡方程,4主矢与主矩均为零 这种情况下，平面任意力系是一个平衡力系。总之，对不同的平面任意力系进行简化综合后结果只有三种可能：(1)合力；(2)合力偶；(3)平衡。,第 4章 平面力系的简化与平衡方程,平面任意力系的解析平衡条件,平面任意力系的一般简化结果为一个主矢 FR和一个主矩Mo。当物体平衡时，主矢和主矩必须同时为零。,由主矢

11、FR=0，,得：,由主矩 Mo=0，得：,第 4章 平面力系的简化与平衡方程,4-3 平面任意力系的平衡条件 平衡方程,平面任意力系的主矢和主矩同时为零FR0，Mo=0是平面任意力系平衡的充要条件。平面任意力系下的解析平衡条件为：力系中所有各力在两个任选坐标轴中每一轴上的投影代数和分别等于零，以及各力对任意一点的矩的代数和等于零。即必须满足下式。其中O是平面内任意一点。三者必须同时为零才能平衡，,三个平衡条件互相独立，对于一个研究对象可以求解三个未知力，且最多求解三个未知力。,第 4章 平面力系的简化与平衡方程,方程组：两个投影方程一个取矩方程，称为一矩式平衡方程。,应用平衡条件求解未知力的步

12、骤为：1、确定研究对象，画受力图；2、由平衡条件建立平衡方程；3、由平衡方程求解未知力。,第 4章 平面力系的简化与平衡方程,例 1 已知 q=2KN/m，求图示结构A支座的反力。,解：取AB 杆为研究对象画受力图。,由 FX=0：,由 Fy=0：,由 MA=0（MB=0也可以）：,第 4章 平面力系的简化与平衡方程,例 2 求图示结构的支座反力。,解：取AB 杆为研究对象画受力图。,由 FX=0：,由 Fy=0：,由 MA=0：,第 4章 平面力系的简化与平衡方程,由 Fy=0：,由 MA=0：,由 FX=0：,例 3 求图示结构的支座反力。,解：取整个结构为研究对象画受力图。,第 4章 平

13、面力系的简化与平衡方程,例 图示构件的A端为固定端，B端自由，求在已知外力的作用下，固定端A的约束力。,第 4章 平面力系的简化与平衡方程,第 4章 平面力系的简化与平衡方程,解:(1)取分离体，作受力图。取构件AB为分离体，其上除作用有已知主动力外，固定端约束力为FAx、FAy和约束力偶MA。(2)列平衡方程，求解未知量。取坐标轴如图所示。一般选取未知力交点为矩心，力求减少每一平衡方程中未知力的数目。否则平衡方程中的项数增多，需要求解联立方程。因为力偶在任何轴上的投影为零，所以投影方程为,FAxF，FAy=2F，MA=2.5Fa,例 起重机重Pl10 kN，可绕铅直轴AB转动；起重机的挂钩上

14、挂一重为P2=40 kN的重物。如图所示。起重机的重心C到转动轴的距离为1.5m、其他尺寸如图所示。求在止推轴承A和轴承B处的约束力。,第 4章 平面力系的简化与平衡方程,分析：以起重机（可看作刚架结构）为研究对象，它所受的主动力有P1和P2。根据对称性，约束力和主动力都位于同一平面内。止推轴承A处有两个约束力FAx，FAy，轴承B处只有一个与转轴垂直的约束力FB，约束力方向如图所示。,刚结点,第 4章 平面力系的简化与平衡方程,取坐标系如图所示，列平面任意力系的平衡方程，即FAy=50 kN,FB=-31 kN,FAx=31 kNFB为负值，说明它的方向与假设的方向相反，即应指向左。,二矩式

15、平衡方程的形式其中矩心A和B两点连线不能与x轴垂直。右端 方程组也是平而任意力系平衡的充要条件，作为平衡的必要条件，是十分明显的。那么充分性如何呢？力系满足条件 MA=0，说明该力系不可能简化为一个力偶，只能是通过点A的一合力，或者平衡。若力系同时又满足条件MB=0，则该力系只能简化成通过A、B两点的合力。当力系又满足Fx0(或Fy0)，其中x(或y)轴不与A、B两点连线垂直，则由右图可知，合力FR这必定为零，这就排除了力系有合力的可能性。由此断定，当二矩式的三个方程同时满足时，力系一定是平衡力系。但须注意，二矩式作为平衡的必要与充分条件是有附加要求的。如果x轴垂直矩心A、B两点的连线，即便三

16、个方程式被满足，力系仍可能有通过两个矩心的合力，而不一定是平衡力系。这时，三个方程不是相互独立的。,第 4章 平面力系的简化与平衡方程,x,O,FR,A,B,三矩式平衡方程的形式其中A、B、C三点不能共线。,第 4章 平面力系的简化与平衡方程,第 4章 平面力系的简化与平衡方程,平面任意力系的平衡方程汇总：,A、B 的连线不和x 轴相垂直。,A、B、C 三点不共线。,一矩式二矩式三矩式,求解技巧 尽量取未知力的交点为矩心，力求减少每一平衡方程中未知力的数目。否则，不但平衡方程中的项数增多，而且导致求解联立方程，增大计算工作量。根据求解方便，还可以采用平面任意力系的二矩式和三矩式形式的平衡方程。

17、,第 4章 平面力系的简化与平衡方程,补充例题学习.PPT,5平面力系的特殊情况 平面一般力系是平面力系的一般情况。平面汇交力系、平面力偶系、平面平行力系都可以看成平面一般力系的特殊情况，它们的平衡方程都可以从平面一般力系平衡方程得到。,第 4章 平面力系的简化与平衡方程,例 十字交叉梁用三个链杆支座固定，如图所示。求在水平力F的作用下各支座的约束力。,第 4章 平面力系的简化与平衡方程,第 4章 平面力系的简化与平衡方程,解：(1)取分离体，作受力图。取十字交叉梁为分离体，其上受主动力F、约束力FA、FB、FC的作用。(2)列平衡方程，求解未知力。用二矩式平衡方程求解：分别以反力FC和FB的

18、交点L和点B为矩心，列平衡方程,如果投影方程选用x轴方向合力为0，就违背了二矩式平衡方程的附加条件，方程中不包含FB，故不能求出FB的值。,第 4章 平面力系的简化与平衡方程,用三矩式平衡方程求解：取L、K、A三点为矩心，列平衡方程,4-4 平面平行力系 平面平行力系是指其各力作用线在同一平面内并相互平行的力系，选择Oy轴与力系中的各力平行，则各力在x轴上的投影恒为零，平衡方程只剩下两个独立的方程。,式中A、B两点连线不与各力作用线平行。平面平行力系只有两个独立的平衡方程，只能求解两个未知量。,第 4章 平面力系的简化与平衡方程,例 塔式起重机如图所示。机架自重P=700kN，作用线通过塔架轴

19、线。最大起重量W=200kN，最大吊臂长为12m，平衡块重为Q，它到塔架轴线的距离为6m。为保证起重机在满载和空载时都不翻倒，试求平衡块的重量Q应为多大。,第 4章 平面力系的简化与平衡方程,解(一)取分离体，作受力图。取起重机为分离体，其上作用有主动力P、W、Q。约束反力为两个轨道的反力NA和NB。这些力组成平行力系。(2)列平衡方程，求解未知力。从受力图上看，NA、NB和Q三个力都是未知的，独立的平衡方程只有两个，求解时需利用塔架翻倒条件建立补充方程。当起重机满载时，起重机最大起吊重量W200kN，这时，平衡块的作用是不使塔架绕B轮翻倒。研究即将翻倒尚未翻例的临界平衡状态，则有补充方程NA

20、=0。在该平衡状态下求得的力Q值，是满载时使塔架不翻倒的最小值，用Qmin来表示。列平衡方程,第 4章 平面力系的简化与平衡方程,当起重机空载时，W0。这时平衡块不能过重，以免使起重机绕A轮翻倒。研究即将倒尚未翻倒的临界平衡状态，有补充方程NB=0。在这个平衡状态下求得的Q值，是空载时使塔架不翻倒的最大值，用Qmax来表示。列平衡方程,从对空载和满载两种临界平衡状态的研究得知，为使起重机在正常工作状态下不翻倒，平衡块重量的取值范围是：75kNQ350kN 在工程实践中，意外因素的影响是难免的，为保障安全工作，应用中需要把理论计算的取值范围适当地缩小。,第 4章 平面力系的简化与平衡方程,物体系

21、的平衡与静不定问题的概念,一、几个概念：1、物体系 由若干个物体通过约束组成的系统2、外 力 物体系以外任何物体作用于该系统的力3、内 力物体系内部各物体间相互作用的力二、物体系平衡方程的数目：由n个物体组成的物体系，总共有不多于3n个独立的平衡方程。工程中，如组合构架、三铰拱等结构，都是由几个物体组成的系统。当物体系平衡时，组成该系统的每一个物体都处于平衡状态，因此对于每一个受平面任意力系作用的物体均可写出三个平衡方程。如物体系由n个物体组成，则共有3 n个独立方程。当系统中有的物体受平面汇交力系或平面平行力系作用时，则系统平衡方程数目相应减少。,物体系的平衡与静不定问题的概念,三、静定与静

22、不定（超静定）概念：当系统中的未知量数目等于独立平衡方程的数目时，则所有未知数都能由平衡方程求出，这类问题称为静定问题。在工程实际中，有时为了提高结构的刚度和坚固性，常增加多余约束，因面使这些结构的未知量的数目多于平衡方程的数目，未知量就不能全部由平衡方程求出，这样的问题称为超静定或静不定问题。对于超静定问题，必须考虑物体因受力作用而产生的变形，加列某些补充方程后，才能使方程的数目等于未知量的数目。超静定问题已超出刚体静力学的范围须在材料力学和结构力学中研究。1、静定问题 当系统中未知量数目等于或少于独立平衡方程数目时的问题。2、静不定问题 当系统中未知量数目多于独立平衡方程数目时，不能求出全

23、部未知量的问题。,物体系的平衡与静不定问题的概念,静定与静不定结构问题例子,平面汇交力系，平面平行力系，平面任意力系,物体系的平衡与静不定问题的概念,梁由两部分铰接组成，每部分有3个平衡方程，共有6个平衡方程。未知量：3个约束力和1个约束力偶铰链C处的2个未知力，共计6个。因此，静定。若将B处的滚动支座改为固定铰支，则系统共有7个未知数，因此系统将是超静定的。,4-5 物体系统的平衡问题 物体系统：在工程中常常将若干构件通过某种连接方式组成机构或结构，用以传递运动或承受荷载。这些机构或结构统称为物体系统。（前面第2章中介绍过）进行力学计算时，首先要对物体系统和系统中的单个构件进行受力分析。以上

24、讨论的都是单个物体的平衡问题。对于物体系统的平衡问题，其要点在于如何正确选择研究对象，一旦确定了研究对象，则计算步骤与单个物体的计算步骤完全一样。下面举例讲解如何正确选择研究对象的问题。,第 4章 平面力系的简化与平衡方程,一个研究对象最多有三个平衡条件，因此研究对象上最多只能有三个未知力。注意到BC杆有三个未知力，而AB 杆未知力超过三个，所以应先取BC 杆为计算对象，然后再取AB 杆为计算对象。,例 4 求图示结构的支座反力。,解：,第 4章 平面力系的简化与平衡方程,由 FX=0：,由 Fy=0：,由 MB=0：,BC杆：,第 4章 平面力系的简化与平衡方程,由 FX=0：,由 Fy=0

25、：,由 MA=0：,AB杆：,注意作用与反作用关系，所以：,第 4章 平面力系的简化与平衡方程,例 5 求图示三铰拱的支座反力。,由 Fy=0：,由 MA=0：,由 FX=0：,第 4章 平面力系的简化与平衡方程,由 MC=0：,取右半部分为研究对象，画受力图：,将FBX 代入式：,即：,得：,第 4章 平面力系的简化与平衡方程,例 由折杆AC和BC铰接组成的厂房刚架结构如图所示，求固定铵支座B的约束力。,第 4章 平面力系的简化与平衡方程,分析：作出整体和各局部(构件AC和BC)受力图，如图所示。待求未知力FBx,FBy出现在图a和图c上，可断定将从这两个受力图上求得待求未知力。观察图a，其

26、上有四个未知力：FAx,Fay，FBx,FBy。三个独立的平衡方程不可能求出四个未知力。对三个力汇交点A写取矩方程可求出待求力FBy。观察图c，其中也有四个未知力：FCx,FCy，FBx,FBy。对图c只能写出三个独立的平衡方程，不可能求出四个未知力。但若能从其他受力图上先求出这四个未知力中的某一个后，则另外三个未知力就可全部求出。本题需要分两步求解。先 从受力图a上求出FBy，再从受力图c上求出FBx。,解 作出整体和各局部(构件AC和BC)受力图，如图所示。第一步：取整体为分离体，其受力图见图a，列平衡方程第二步；取BC构件为分离体，其受力见图c，列平衡方程,第 4章 平面力系的简化与平衡

27、方程,例 如图所示结构由杆件AB、BC、CD、圆轮O、软绳和重物E组成。圆轮与杆CD用铰链连接，圆轮半径r=l2。物E重为W，其他构件不计自重。求固定端A的约束力。,第 4章 平面力系的简化与平衡方程,第 4章 平面力系的简化与平衡方程,解：作出整体和各局部的受力图a、b、c。BC杆为二力杆，不必作出受力图。轮O和重物E不必单独作出受力图，将它们与联结滑轮的构件CD放在一起作受力图。分析：待求量FAx、FAy、MA出现在图a和图b上，可断定将从这两个受力图上求得待求量。观察图a，其上有五个未知量。只有从其他受力图上求出固定铰支座D的约束力后才能从图a上求出待求量。观察图b，其上有四个未知量。只

28、有从其他受力图上求出圆柱铰链B的约束力FB，就可从图b求出待求量。因为从图a和图b上都不能直接解出待求量，再来观察图c。其上有三个未知力：FC、FDx,FDy，可写出三个平衡方程，解出这三个未知力。FC=FB。,第 4章 平面力系的简化与平衡方程,本题有两种求解方案：一是从图c上求出FC，再从图b上求出A端反力；另一是从图c上求出FDx、FDy：再从图a上求出A端反力。第一方案需用四个平衡方程，第二方案需用五个平衡方程。分两步求解：第一步；取杆件CD、圆轮、绳索及重物组成的体系为分离体，列平衡方程求出FC,第二步，取杆件AB为分离体，受力图b，列平衡方程求出待求量,例 图所示结构由折杆AB和B

29、C铰接组成。按图示尺寸和荷载求固定铰支座A的约束力。,第 4章 平面力系的简化与平衡方程,分析：作整体和各局部的受力图a、b、c所示。杆件上的均布荷载用其合力FRl和FR2表示，且FRl=FR2=qa。,第 4章 平面力系的简化与平衡方程,如从整体受力图a上求支座A的约束力，需事先求出链杆支座D或B的反力；如从杆AB受力图b上求支座A的约束力，需要事先求出铰C处的约束力FCx,FCy。两方案都可行。第一步：取构件CD为分离体，受力图。列平衡方程解出FD,第 4章 平面力系的简化与平衡方程,第二步：取整体为分离体，受力图a。列x轴平衡方程求出FAx为求反力FAy，可选反力FB和FD的作用线的交点

30、K为矩心，平衡方程,物体系平衡问题求解思路和注意事项总结(1)选择合适的研究对象 应该针对问题的具体条件和要求，构思合理的解题思路。要在了解整体和各局部受力情况的基础上，恰当选取分离体，恰当选择平衡方程。列方程时，要选择适当的投影轴和矩心，尽量使不需要求的未知量不出现在所列的方程中。,第 4章 平面力系的简化与平衡方程,(2)正确地进行受力分析 物体间作用力方向无法判定时，可先假定，求解结果为正说明假设方向一致，结果为负说明假设方向相反。对于作用力与反作用力，可先假定其中之一，另一个按照相反方向施加。(3)正确区分内力和外力(4)注意应用平衡概念考察整体与局部受力状态 物体系是由多个物体所组成

31、，求解过程中一般都要选取两次以上的分离体，才能解出所要求的未知量。,第 4章 平面力系的简化与平衡方程,第 4章 平面力系的简化与平衡方程,求解静定物体系的平衡问题时，可以选每个物体为研究对象，列出全部平衡方程，然后求解：也可先取整个系统为研究对象，列出平衡方程，这样的方程因不包含内力，式中未知量较少，解出部分未知量后，再从系统中选取某些物体作为研究对象，列出另外的平衡方程直至求出所有的未知量为止。在选择研究对象和列平衡方程时，应使每一个平衡方程中的未知量个数尽可能少，最好是只含有一个未知量，以避免求解联立方程。,物体系的平衡问题补充例题,例 下图所为钢结构拱架，拱架由两个相同的钢架AC和BC

32、铰接，吊车梁支承在钢架的D,E上。设两钢架各重为P=60 kN，吊车梁重为Pl=20 kN，其作用线通过点C；载荷为P2=10 kN；风力F=10 kN。尺寸如图所示。D，E两点在力P的作用线上。求固定铰支座A和B的约束力。,物体系的平衡问题补充例题,解：(1)选整个拱架为研究对象。拱架在主动力P，P1，P2，F和铰链A，B的约束力FAx，FAy，FBx，FBy作用下平衡，受力如图a所示。列出平衡方程：以上三个方程包含四个未知数，欲求得全部解答，必须再补充方程。,物体系的平衡问题补充例题,(2)选右边钢架为研究对象其受力如图b。为了减少方程中的未知量数目采用力矩方程，即这时又出现了一个未知数F

33、E。为求得该力的大小，可再考虑吊车梁的平衡。,物体系的平衡问题补充例题,3)选吊车粱为研究对象。受力如图c所示。为求得FE，列如下方程：,由式(e)解得由式(a)求得将FBy和FE的值代入式(d)得代入式(b)得代入式(c)得,解：1、取AC 段研究，受力分析如图。,例题 三铰拱桥如图所示，由左右两段借铰链C 连接起来，又用铰链A、B 与基础相联结。已知每段重G=40 kN，重心分别在D、E 处，且桥面受一集中载荷P=10 kN。设各铰链都是光滑的，试求平衡时，各铰链中的力。尺寸如图所示，单位是 m。,物体系的平衡问题补充例题,列平衡方程：,2、再取BC 段研究，受力分析如图。,列平衡方程：,

34、物体系的平衡问题,B,C,E,联立求解：可得 FAx=-FBx=FCx=9.2 kN FAy=42.5 kN FBy=47.5 kN FCy=2.5 kN,FCx 和 FCx、FCy 和 FCy是二对作用与反作用力。,物体系的平衡问题,解：1、取CE 段为研究对象，受力分析如图。,P,例题 组合梁AC 和CE 用铰链C 相连，A端为固定端，E 端为活动铰链支座。受力如图所示。已知：l=8 m，P=5 kN，均布载荷集度q=2.5 kN/m，力偶矩的大小M=5kNm，试求固端A、铰链C 和支座E 的反力。,物体系的平衡问题,列平衡方程：,2、取AC 段为研究对象，受力分析如图。,联立求解：可得 FE=2.5 kN（向上）FC=2.5 kN（向上）,物体系的平衡问题,列平衡方程：,联立求解：可得 MA=30 kNm FA=-12.5 kN,物体系的平衡问题,精品课件！,精品课件！,Thanks to everybody,4-6 考虑摩擦的平衡问题本节由同学们自学,