因式分解总复习ppt课件.ppt

《因式分解总复习ppt课件.ppt》由会员分享，可在线阅读，更多相关《因式分解总复习ppt课件.ppt（60页珍藏版）》请在三一办公上搜索。

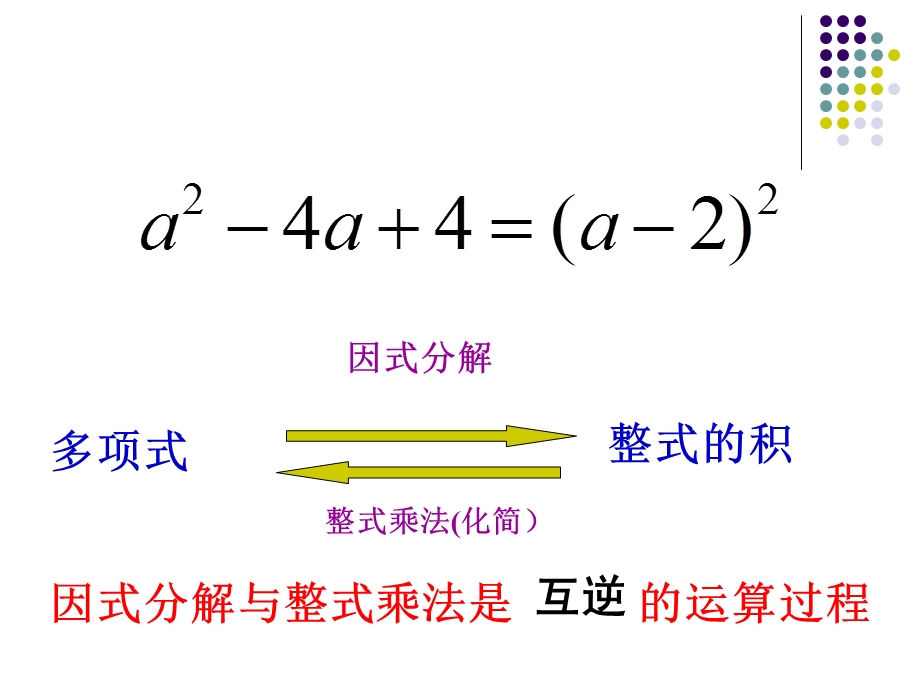
1、,因式分解总复习,把一个多项式写成几个整式的积的形式叫做因式分解.,1.下列从左到右的变形中，是因式分解的是（ ）,D,也叫把多项式分解因式,整式的积,多项式,整式乘法(化简）,因式分解,因式分解与整式乘法是 的运算过程,互逆, x(x-1)=x-x； ( ) ( ) x+2x=x(x+2)； ( ) a+1=a(a+ ). ( ),2.辩一辨下列从左边到右边的变形 哪些是属于因式分解？,X,X,X, x+2x+1=x(x+2)+1 ( ) y-4=(y+2)(y-2)； ( ),X,3.我们学了哪些常用的因式分解的方法？,（1）提公因式法 （2）公式法,（3）十字相乘法（4）分组分解法,一、

2、提公因式法,例1、 中各项的公因式是_。,：一个多项式每一项都含有的相同的因式， 叫做这个多项式各项的公因式。,3xy2,找公因式的方法：1）、系数 ； 2）、字母是 ；3）、字母的次数 。,各系数的最小公倍数,相同字母,相同字母的最低次数,：就是将多项式的所有公有因式全部提 出来作为一个因式，其他因子作为另一个因式的方法,公因式,提公因式法,4、 指出下列多项式中各项的公因式,(1)ax+ay,(2)3mx-6mxy,(5)4(a+b)2-10(a+b),(4)12x3y5z-9x4y3+3x2y2,a,mx,数字因数也是公因式,x,(3)-8x2y+6xy,2xy,(a+b),各项系数的最

3、大公约数,找各项的相同字母，各字母的指数 是取各项该字母 的最低次数。,如何找公因式？,字母：,系数：,3,2,3,2,y,2,经常使得提取后的首项系数为正！,(或一个整体）,5、下列提公因式法因式分解正确吗？不对的给予改正。,漏项；,变错符号,分解不彻底；,混淆因式分解与整式乘法的意义。,(5) x2(x-y)+y2(y-x)=x2(x-y)-y2(x-y) =(x2-y2)(x-y)=(x-y)(x+y)(x-y),结论不规范,+1,-,=(x-y)2(x+y),（xy）与（yx）要先统一公因式,6、用提取公因式法对下列各式进行因式分解：,二 公式法1,a2b2（ab）（ab）,1、有且只

4、有两个平方项；2、两个平方项异号。,能使用平方差公式分解因式的多项式的特点：, 平方差公式 因式分解,逆用乘法公式将多项式分解因式的方法叫公式法,常用的有平方差公式法和完全平方公式法,用语言叙述为：如果一个二项式，它能够化成两个整式的平方的差，就可以用平方差公式分解因式，分解成两个整式的和与差的积.,7.辨一辨 下列多项式可以用平方差公式分解因式吗？,判一判！,=(x-y)2-4(x+y)2=(x-y)+2(x+y)(x-y)-2(x+y)=(3x+y)(-x-3y),=-(3x+y)(x+3y),因式分解,(2),变式：,=（n+m)(n-m),=(m2+n2)(m2-n2),=(m2+n2

5、)(m+n)(m-n),=（m+n)+(m-n)(m+n)-(m-n),=4mn,=5(m+n)+4(m-n)5(m+n)-4(m-n),=(9m+n)(m+9n),二、公式法2,a2 2ab b2 （ab）2 a2 2ab+ b2 （ab）2,能使用完全平方公式分解因式的多项式的特点：,1、共有三项，有两个是平方项；2、两个平方项同号。3、含有交叉项的正负2倍。, 完全平方公式法因式分解 ,用语言叙述为：两个数的平方和，加上（或减去）这两数的乘积的2倍，等于这两个数的和（或差）的平方. （首平方尾平方，两倍乘积中间放）,8、判断下列多项式是不是完全平方式,因式分解,变式：,(3),=b(a2

6、-6a+9)=b(a-3)2,=(a-1-3)2=(a-4)2,=(a2-1)2-6(a2-1)+9,=(a2-1-3)2,=(a2-4)2,=(a+2)2(a-2)2,9、用公式法对下列各式进行因式分解：,因式分解的一般步骤：,第一步：先看多项式各项有无公因式， 如有公因式则要先提取公因式；,第二步：再看有几项（包括一些变形后的多项式）， 如两项，则考虑用平方差公式； 如三项，则考虑用完全平方公式；,第三步：最后看各因式能否再分解， 如能分解，应分解到不能再分解为止。,总结经验：分解因式三步曲,先看有无公因式,再看能否套公式,：将因式分解进行到底.,目标,1.把下列各式分解因式：,特别要注意

7、一些变形后的多项式的分解；要注意分析是否完成因式分解,2、巧算：,求,3.（1）已知：,的值。,分析：题意就是将 因式分解,3.（2）、讨论：已知m、n是矩形的长和宽，且 m、n为正整数，满足m2=n2+45，求这个矩形的面积。,其实就是将m2-n2因式分解，再对45分解素因数,今天，我们复习了分解因式的哪些知识？,因式分解,思想方法上：整体思想和转化思想,总结经验：分解因式三步曲,先看有无公因式,再看能否套公式,努力达到:将因式分解进行到底.,十字相乘试一试,分组分解要合适,一、首项有负常提负,二、各项有公先提公,三、某项提出莫漏1,四、括号里面分到“底”。,因式分解的“四个注意”,1.(x

8、+2)(x+1)=,x2+3x+2,3.(x-2)(x+1)=,x2-x-2,4.(x-2)(x-1)=,x2-3x+2,2.(x+2)(x-1)=,x2+x-2,5.(x+2)(x+3)=,x2+5x+6,6.(x+2)(x-3)=,x2-x-6,7.(x-2)(x+3)=,x2+x-6,8.(x-2)(x-3)=,x2-5x+6,(x+a)(x+b),=x2+(a+b)x+ab,请直接口答计算结果：,(x+2)(x+1),x2+3x+2,(x-2)(x+1),x2-x-2,(x-2)(x-1),x2-3x+2,(x+2)(x-1),x2+x-2,(x+2)(x+3),x2+5x+6,(x+

9、2)(x-3),x2-x-6,(x-2)(x+3),x2+x-6,(x-2)(x-3),x2-5x+6,(x+a)(x+b),=,x2+(a+b)x+ab,=,=,=,=,=,=,=,=,1.,2.,3.,4.,5.,6.,7.,8.,试一试,分解因式:x2+4x+3=x2-2x-3=,利用十字交叉线来分解系数，把二次三项式分解因式的方法叫做十字相乘法.,1.x2+8x+12=,2.x2-11x-12=,练一练,3.x2-7x+12=,4.x2-4x-12=,(x+2)(x+6),(x-6)(x+2),(x-3)(x-4),(x-12)(x+1),符号规律： 常数项是正数时，应分解为两个 因数

10、，他们的符号与一次项系数符号 ； 常数项是负数时，应分解为两个 因数，其绝对值 的因数与一次项系数的符号相同.,同号,相同,异号,较大,5.x2+13x+12=,(x+1)(x+12),6.x2-x-12=,(x-4)(x+3),将下列各式因式分解:,x2+px+q=,x2+(a+b)x+ab=,x,x,a,b,ax,+,bx,=,(a+b)x,(x+a)(x+b),课堂小结,对二次三项式x2+px+q进行因式分解，应重点掌握以下三个问题：,1.掌握方法：拆分常数项，验证一次项.,2.符号规律： 当q0时，a、b同号，且a、b的符号与p的符号相同； 当q0时，a、b异号，且绝对值较大的因数与p

11、的符号相同.,3.书写格式：竖分横积,用十字相乘法进行因式分解：,(x+2)(x-3),1.x2-x- 6 =,(x-3)(x+5),2.x2+2x-15=,(x+2)(x-5),3.x2-3x-10=,(x-5)(x-4),4.x2-9x+20=,(x-7)(x+4),5.x2-3x-28=,(x+2)(x-4),6.x2-2x-8=,(x-1)(x-3),7.x2-4x+3=,(x+3)(x+4),(x+2)(x+3),(x-3)(x+7),8.x2+7x+12=,9.x2+5x+6=,(y+12)(y-3),(y-9)(y+14),(y+4)(y-15),(y-7)(y+16),(y-8

12、)(y-17),(y+16)(y+3),(y+19)(y-7),(y+11)(y-10),(y-13)(y-3),(y+14)(y+4),先填空，再分解（尽可能多的） 2 ( )=( )( ),拓展练习,因式分解,分组分解法,因式分解,复习(1)6a3-8a2-4a (2) x3y2- xy3(3) -x3y3-x2y2+xy (4) -12a2m+1bm+2+20am+1b2m+4,解原式=2a(3a2-4a-2),解原式= xy2( x2-y),解原式=-xy(x2y2+xy-1),解原式=-4am+1bm+2(3am-5bm+2),(3) -x3y3-x2y2+xy (4) -12a2m

13、+1bm+2+20am+1b2m+4,因式分解,解原式=-xy(x2y2+xy-1),解原式=-4am+1bm+2(3am-5bm+2),因式分解时，应首先考虑能否提取公因式，能提取公因式的，要先提取公因式而后考虑继续分解，公因式的符号一般应与多项式的首项的符号相同。,解原式=-xy(x2y2+xy-1),因式分解,(3) -x3y3-x2y2+xy,提取公因式后，括号内的项数同多项式本身的项数必须相同，当公因式为多项式的某一项时，则括号必有1这一项，这个1不能漏掉。,解原式,因式分解,(5) 6ax-9ay+2bx-3by,=,?,因式分解,分组分解法,因式分解,将下列各式用分组分解法因式分

14、解,(a + b )2 - a - b,解原式 = (a + b )2 - (a + b),=(a + b)( a + b - 1),因式分解,找规律,分组,ma - mb + m2 + mn + na - nb,解原式=(ma + na) - (mb + nb) + (m2 + mn),= a(m + n) - b(m + n) + m(m + n),= (m + n)(a - b + m),因式分解,用两种分组方法将下列各式因式分解,2a2 - ab + 2ac - bc,解原式=(2a2-ab)+(2ac-bc),= a(2a-b)+ c(2a-b),= (2a-b)(a+c),解原式=

15、(2a2+2ac)-(ab+bc),= 2a(a+c)- b(a+c),= (a+c)(2a-b),因式分解,-4yz + 3x2 - 2xz + 6xy,解原式 = (6xy - 4yz) + (3x2 - 2xz),= 2y(3x - 2z) + x(3x - 2z),= (3x - 2z)(2y + x),因式分解,-4yz + 3x2 - 2xz + 6xy,解原式 = (6xy - 4yz) + (3x2 - 2xz),= 2y(3x - 2z) + x(3x - 2z),= (3x - 2z)(2y + x),解原式 = (6xy + 3x2) - (4yz + 2xz),= 3x

16、(2y + x) - 2z(2y + x),= (2y + x)(3x - 2z),因式分解,分 析在用分组分解法因式分解时，要注意分组不能使一个多项式变为乘积形式，分组的目的是分好的各组能提取各自的公因式同时使各组提取公因式后剩下的多项式又是各组的公因式，可以再提取，从而使问题得到解决，上述规律可以通俗的归纳成：“分组的目的是为了提取，提取的目的是为了再提取”。,因式分解,将下列各式用分组分解法因式分解练习1: ax + bx + cx + ay + by + cy,练习1: ax + bx + cx + ay + by + cy 解原式 = x(a + b + c) + y(a + b +

17、 c) = (a + b + c)(x + y),因式分解,将下列各式用分组分解法因式分解练习1: ax + bx + cx + ay + by + cy 解原式 = x(a + b + c) + y(a + b + c) = (a + b + c)(x + y),解原式 = a(x + y) + b(x + y) + c(x + y) = (x + y)(a + b + c),因式分解,练习2: ab + ac + 2a + bx + cx + 2x,解原式 = a(b + c + 2) + x(b + c + 2),= (b + c + 2)(a + x),因式分解,练习2: ab + a

18、c + 2a + bx + cx + 2x 解原式 = a(b + c + 2) + x(b + c + 2) = (b + c + 2)(a + x),解原式 = b(a + x) + c(a + x) + 2(a + x),= (a + x)(b + c + 2),因式分解,练习3: mx + mx2 - n - nx,解原式 = mx(x + 1) - n(x + 1),= (x + 1)(mx - n),因式分解,练习3: mx + mx2 - n - nx 解原式 = mx(x + 1) - n(x + 1) = (x + 1)(mx - n),解原式 = (mx - n) + x(

19、mx - n),= (mx - n)(x + 1),因式分解,练习4: ab + a + b + 1,解原式 = a(b + 1) + (b + 1),= (b + 1)(a + 1),因式分解,练习4: ab + a + b + 1 解原式 = a(b + 1) + (b + 1) = (b + 1)(a + 1),解原式 = b(a + 1) + (a + 1),= (a + 1)(b + 1),因式分解,练习5: ab - 1 + a - b,解原式 = a(b + 1) - (b + 1),= (b + 1)(a - 1),因式分解,练习5: ab - 1 + a - b 解原式 =

20、a(b + 1) - (b + 1) = (b + 1)(a - 1),解原式 = b(a - 1) + (a - 1),= (a - 1)(b + 1),解原式 = (m3 - 5) + 4m(m3 - 5),因式分解,练习6: m3 + 4m4 - 5 - 20m,= (m3 - 5)(1 + 4m),因式分解,练习6: m3 + 4m4 - 5 - 20m解原式 = (m3 - 5) + 4m(m3 - 5) = (m3 - 5)(1 + 4m),解原式= m3(1 + 4m) - 5(1 + 4m),= (1+4m)(m3 - 5),因式分解,练习7: 3x3 + 6x2y - 3x2

21、z - 6xyz,解原式 = 3x(x2 + 2xy - xz - 2yz),= 3x(x2 + 2xy) - (xz + 2yz),= 3xx(x + 2y) - z(x + 2y),= 3x(x + 2y)(x - z),3x,因式分解,练习8: ax5 - ax4 + ax - a,解原式 = a(x5 - x4 + x - 1),= ax4(x - 1) + (x - 1),= a(x - 1)(x4 + 1),练习9: ax2 - bx2 - bx + ax + b - a解原式 = x2(a - b) + x(a - b) - (a - b) = (a - b)(x2 + x - 1),因式分解,解原式= a(x2 + x - 1) - b(x2 + x - 1),= (x2 + x - 1)(a - b),