带电粒子在匀强磁场中的运动(含各种情况)ppt课件.ppt

《带电粒子在匀强磁场中的运动(含各种情况)ppt课件.ppt》由会员分享，可在线阅读，更多相关《带电粒子在匀强磁场中的运动(含各种情况)ppt课件.ppt（58页珍藏版）》请在三一办公上搜索。

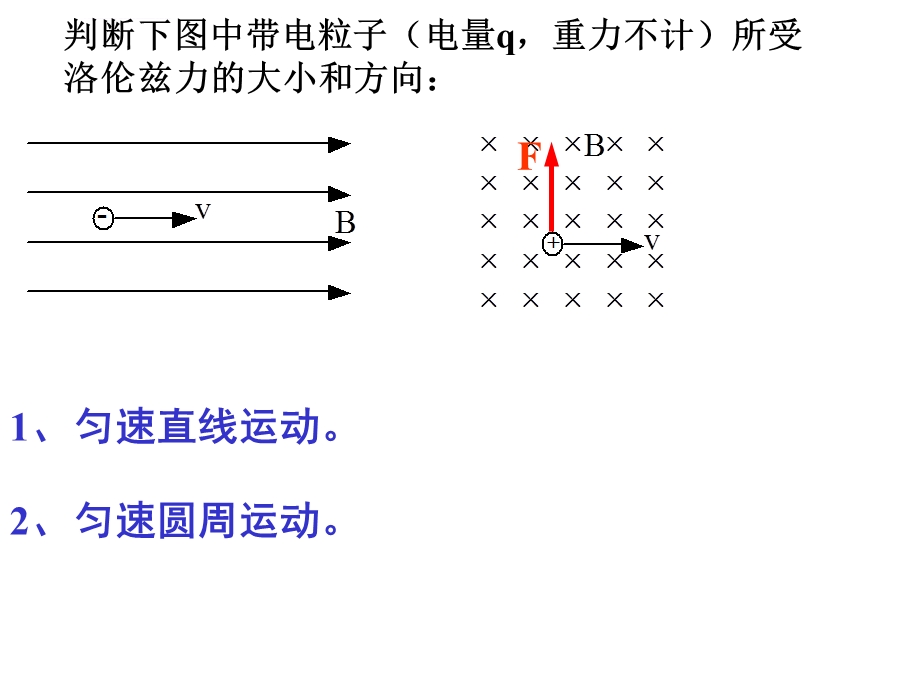
1、带电粒子在匀强磁场中的运动,带电粒子在磁场中的运动形式,判断下图中带电粒子（电量q，重力不计）所受洛伦兹力的大小和方向：,1、匀速直线运动。,2、匀速圆周运动。,带电粒子在匀强磁场中做匀速圆周运动，洛伦兹力就是它做圆周运动的向心力,请你推导半径和周期表达式。,实验演示,3、粒子运动方向与磁场有一夹角（大于0度小于90度）轨迹为螺线,1、如图所示，一束电子（电量为e）以速度v垂直从A点射入磁感应强度为B，宽度为d的匀强磁场中，且与磁场的边界垂直，通过磁场时速度方向与电子原来入射方向的夹角是30，则：电子的质量是 ，通过磁场的时间是 。,一、磁场作用下粒子的偏转,2、如图所示，在半径为R 的圆的范

2、围内，有匀强磁场，方向垂直圆所在平面向里一带负电的质量为m电量为q粒子，从A点沿半径AO的方向射入，并从C点射出磁场AOC120o则此粒子在磁场中运行的时间t_(不计重力),3 . 图中MN表示真空室中垂直于纸面的平板，它的一侧有匀强磁场，磁场方向垂直纸面向里，磁感应强度大小为B 。一带电粒子从平板上的狭缝O处以垂直于平板的初速v射入磁场区域，最后到达平板上的P 点。已知B 、v以及P 到O的距离l 不计重力,求此粒子的电荷q与质量m 之比。,4、长为L的水平极板间，有垂直纸面向内的匀强磁场，如图所示，磁场强度为B，板间距离也为L，板不带电，现有质量为m，电量为q的带正电粒子（不计重力），从左

3、边极板间中点处垂直磁场以速度v平行极板射入磁场，欲使粒子不打在极板上，则粒子入射速度v应满足什么条件？,1.如图，虚线上方存在无穷大的磁场，一带正电的粒子质量m、电量q、若它以速度v沿与虚线成300、600、900、1200、1500、1800角分别射入，请你作出上述几种情况下粒子的轨迹、并求其在磁场中运动的时间。,二、有界磁场问题：,粒子在磁场中做圆周运动的对称规律： 从同一直线边界射入的粒子， 从 同一边界射出时，速度与边界的夹角相等。,1、两个对称规律：,入射角300时,入射角1500时,4、如图所示，在第一象限有磁感应强度为B的匀强磁场，一个质量为m，带电量为+q的粒子以速度v从O点射

4、入磁场，角已知，求粒子在磁场中飞行的时间和飞离磁场的位置（粒子重力不计）,2、如图所示，在y0的区域内存在匀强磁场，磁场方向垂直纸面向外，磁感应强度为B。一个正电子以速度v从O点射入磁场，入射方向在xy平面内，与x轴正向的夹角为。若正电子射出磁场的位置与O点的距离为L，求正电子的电量和质量之比？,思考：如果是负电子,那么，两种情况下的时间之比为多少？,3、如图所示，在半径为r的圆形区域内，有一个匀强磁场，一带电粒子以速度v0从M点沿半径方向射入磁场区，并由N点射出，O点为圆心，MON=120，求粒子在磁场区的偏转半径R及在磁场区中的运动时间。（粒子重力不计）,圆形磁场区 。画好辅助线（半径、速

5、度、轨迹圆的圆心、连心线）,偏角：,经历时间：,注意：对称性，在圆形磁场区域内，沿径向射入的粒子，必沿径向射出。,4、电视机的显像管中，电子束的偏转是用磁偏转技术实现的。电子束经过电压为U的加速电场后，进入一圆形匀强磁场区，如图所示。磁场方向垂直于圆面。磁场区的中心为O，半径为r。当不加磁场时，电子束将通过O 点而打到屏幕的中心M点。为了让电子束射到屏幕边缘P，需要加磁场，使电子束偏转一已知角度，此时磁场的磁感应强度B应为多少？,5、如图所示，比荷为e/m的电子垂直射入宽为d，磁感应强度为B的匀强磁场区域，则电子能穿过这个区域至少应具有的初速度v0大小为多少？,总结：临界条件的寻找是关键。,2

6、、临界问题：,例2：如图所示，匀强磁场的磁感应强度为B，宽度为d，边界为CD和EF。一电子从CD边界外侧以速率V0垂直射入匀强磁,场,入射方向与CD边界间夹角为。已知电子的质量为m，电量为e，为使电子能从磁场的另一侧EF射出，求电子的速率V0至少多大？,（1）速度方向一定，大小不定。,关键：先画圆心轨迹，再画圆轨迹，寻找临界情形。,分析：当入射速率很小时，电子在磁场中转动一段圆弧后又从一侧射出，速率越大，轨道半径越大，当轨道与边界相切时，电子恰好不能从射出，如图所示。电子恰好射出时，由几何知识可得：,例3、一个质量为m，带电量为q的带正电粒子（不计重力）从O点沿y方向以初速度v0射入一个边界为

7、矩形的匀强磁场中，磁场方向垂直于xy平面向内。它的边界分别是y0，ya，x1.5a，x1.5a，如图7所示，改变磁感应强度B的大小，粒子可从磁场的不同边界面射出，并且射出磁场后偏离原来速度方向的角度会随之改变。试讨论粒子可以从哪几个边界射出，从这几个边界面射出时磁感应强度B的大小及偏转角度各在什么范围内？,例4、如图所示，电子源S能在图示纸面上360度范围内发射速率相同的电子（质量为m、电量为e），MN是足够大的竖直挡板，与S的水平距离OS=L，挡板左侧是垂直纸面向里，磁感应强度为B的匀强磁场。,（1）要使放射的电子可能到达挡板，电子的速度至少为多大？,（2）若S发射的电子速率为eBL/m时，

8、挡板被电子击中的范围有多大？,（2）速度大小一定，方向不定。,例5、一匀强磁场宽度d=16cm,磁感应强度B=0.5T，电子源在A点以速度大小v=1.01010m/发射电子，在纸面内不同方向，从A点射入磁场（足够大）中，且在右侧边界处放一荧光屏（足够大），电子的比荷e/m=21011c/kg,求电子打中荧光屏的区域的长度 ？,A,变化：如果在A点左侧无磁场，问题同上。,解：由牛顿第二定律得,R=10cm ,由题意得电子打到荧光屏上的区域为图中BC之间的区域：由几何关系BC=2AB AB= ,代入数据得：BC=16cm,o,o1,例6、一匀强磁场，磁场方向垂直于xy平面，在xy平面上，磁场分布在

9、以O为中心的一个圆形区域内。一个质量为m、电荷为q的带电粒子，由原点O开始运动，初速为v，方向沿x正方向。后来，粒子经过y轴上的P点，此时速度方向与y轴的夹角为30，P到O的距离为L，如图所示。不计重力的影响。求磁场的磁感强度B的大小和xy平面上磁场区域的半径R。,求磁场区域关键在于定圆轨迹。,二、质 谱 仪,例题：一个质量为m、电荷量为q的粒子，从容器下方的小孔S1飘入电势差为U的加速电场，然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中，最后打到照相底片D上（图3.6-4）。求粒子进入磁场时的速率。求粒子在磁场中运动的轨道半径。,质谱仪最初是由汤姆生的学生阿斯顿设计的，他用质

10、谱仪发现了氖20和氖22，证实了同位素的存在。现在质谱仪已经是一种十分精密的仪器，是测量带电粒子的质量和分析同位素的重要工具。,带电粒子在汽泡室运动径迹的照片。有的粒子运动过程中能量降低，速度减小，径迹就呈螺旋形。,三、回 旋 加 速 器,2回旋加速器,1直线加速器,练习：回旋加速器中磁场的磁感应强度为B，D形盒的直径为d，用该回旋加速器加速质量为m、电量为q的粒子，设粒子加速前的初速度为零。求：,（1） 粒子的回转周期是多大？,（2）高频电极的周期为多大？,（3） 粒子的最大动能是多大？,（4） 粒子在同一个D形盒中相邻两条轨道半径之比,三、带电粒子在复合场中的运动,例1、如图所示，实线表示

11、在竖直平面内的匀强电场的电场线，电场线与水平方向的夹角为，水平方向的匀强磁场与电场线正交，有一带电液滴沿斜向上的虚线L做直线运动.L与水平方向的夹角为，且则下列说法中正确的是A.液滴一定做匀速直线运动B.液滴一定带负电C.电场线方向一定斜向下D.液滴也有可能做匀变速直线运动,（1）直线运动的情形：,例2、如图，套在足够长的绝缘直棒上的小球，其质量为m，带电量+q，小球可在棒上滑动，将此棒竖直放在相互垂直，且沿水平方向的匀强电场和匀强磁场中，电场强度为E，磁感应强度为B，小球与棒的动摩擦因数为，求小球由静止沿棒下落的最大加速度和最大速度。,变化4：假如电场反向，判断运动情形。,变化1、小球加速度

12、为最大加速度的一半时的速度。,变化3、小球下滑速度为最大速度一半时的加速度。,变化2、假如 问题同变化1。,变化5、如图所示，质量是m的小球带有正电荷，电量为q，小球中间有一孔套在足够长的绝缘细杆上。杆与水平方向成角，与球的动摩擦因数为，此装置放在沿水平方向、磁感应强度为B的匀强磁场中。若从高处将小球无初速释放，求：小球下滑过程中加速度的最大值和运动速度的最大值。,变化6：如图所示，在空间存在着水平向右、场强为E的匀强电场，同时存在着竖直向上、磁感强度为B的匀强磁场。在这个电、磁场共同存在的区域内有一足够长的绝缘杆沿水平方向放置，杆上套有一个质量为m、带电荷量为q的金属环。已知金属环与绝缘杆间

13、的动摩擦因数为，且mgqE。现将金属环由静止释放，设在运动过程中金属环所带电荷量不变。,(1)试定性说明金属环沿杆的运动情况。,(3)求金属环运动的最大速度的大小。,(2)求金属环运动的最大加速度的大小。,变7带负电的小物体A放在倾角为（sin=0.6）的绝缘斜面上。整个斜面处于范围足够大、方向水平向右的匀强电场中，如图所示。物体A的质量为m，电量为-q，与斜面间的动摩擦因数为，它在电场中受到的电场力的大小等于重力的一半。物体A在斜面上由静止开始下滑，经时间t后突然在斜面区域加上范围足够大的匀强磁场，磁场方向垂直于纸面。磁感应强度大小为B，此后物体A沿斜面继续下滑距离L后离开斜面。,物体A在斜

14、面上的运动情况如何？说明理由。,物体A在斜面上运动过程中由多少能量转化为内能？,例2、如图，PQ为一块长为L，水平放置的绝缘平板，整个空间存在着水平向左的匀强电场，板的右半部分还存在着垂直于纸面向里的有界匀强磁场，一质量为m，带电量为q的物体，从板左端P由静止开始做匀加速运动，进入磁场后恰作匀速运动，碰到右端带控制开关K的挡板后被弹回，且电场立即被撤消，物体在磁场中仍做匀速运动，离开磁场后做匀减速运动，最后停在C点，已知PC=L/4，物体与板间动摩擦因数为,求：（1）物体带何种电荷？（2）物体与板碰撞前后的速度v1和v2（3）电场强度E和磁感应强度B多大？,例3、如图所示，匀强电场的场强E=4

15、V/m，方向水平向左匀强磁场的磁感强度B=2T，方向垂直于纸面向里，一个质量为m=1g、带正电的小物体A从M点沿绝缘粗糙的竖直壁无初速下滑，当它滑行h=0.8m到N点时离开壁做曲线运动，运动到P点时恰好处于平衡状态，此时速度方向与水平成450角，设P与M的高度差H=1.6m，求 （1）A沿壁下滑过程中摩擦力作的功。 （2）P与M的水平距离。,例1、用绝缘细线悬吊着的带正电小球在匀匀强磁场中做简谐运动，则A、当小球每次通过平衡位置时，动能相同B、当小球每次通过平衡位置时，速度相同C、当小球每次通过平衡位置时，丝线拉力相同D、撤消磁场后，小球摆动周期变化,（2）圆周运动情形,例2、如图所示，水平放

16、置的平行金属板 AB间距为 d ，水平方向的匀强磁场为B 。今有一带电粒子在 AB 间竖直平面内作半径为 R 的匀速圆周运动，则带电粒子转动方向为 时针，速率为 。,例3、在光滑绝缘水平面上，一轻绳拉着一个带电小球绕竖直方向的轴O在匀强磁场中做逆时针方向的水平匀速圆周运动，磁场方向竖直向下，其俯视图如图9所示，若小球运动到A点时，绳子突然断开，关于小球在绳断开后可能的运动情况，以下说法正确的是（ ）。,A小球仍做逆时针匀速圆周运动，半径不变B小球仍做逆时针匀速圆周运动，半径减小C小球做顺时针匀速圆周运动，半径不变D小球做顺时针匀速圆周运动，半径减小,例4、在如图所示的直角坐标系中,坐标原点O处

17、固定有正电荷,另有平行于y轴的匀强磁场。一个质量为m带电量为q的微粒,恰能以y轴上P点(0,a,0)为圆心做匀速圆周运动,其轨迹平面与xOz平面平行,角速度为,旋转方向如图中箭头所示,试求匀强的磁感应强度大小和方向。,例5、在竖直放置的光滑绝缘圆环中，套有一个带电荷量为一q、质量为m的小环，整个装置放在如图所示的正交电磁场中，已知E=mg/q当小环从大环顶无初速下滑时，在滑过什么弧度时所受洛仑兹力最大？,例1、如图所示，一个质量为m、带电量为q的正离子，在D处沿着图示的方向进入磁感应强度为B的匀强磁场，此磁场方向垂直纸面向里，结果离子正好从离开A点距离为d的小孔C沿垂直于AC的方向进入匀强电场

18、，此电场方向与AC平行且向上，最后离子打在B处，而B离A点距离为2d（ABAC），不计粒子重力，离子运动轨迹始终在纸面内，求：（1）离子从D到B所需的时间（2）离子到达B处时的动能,（3）多种运动综合。,例2、如图所示，在x轴上方是垂直纸面向里的磁感应强度为B的匀强磁场，在x轴下方是方向与y轴正方向相反的场强为E的匀强电场，已知沿x轴方向跟坐标原点相距为L处有一垂直于x轴的屏MN。现有一质量m、带电荷量为-q的粒子从坐标原点沿y轴正方向射入磁场。如果想使粒子垂直打在光屏MN上，那么：（1）电荷从坐标原点射入时速度应为多大？（2）电荷从射入磁场到垂直打在屏上要用多少时间？,例3、如图所示，在y0

19、的空间中存在匀强电场，场强沿y轴负方向；在y0的空间中，存在匀强磁场，磁场方向垂直xy平面（纸面）向外。一电量为q、质量为m的带正电的运动粒子，经过y轴上yh处的点P1时速率为v0，方向沿x轴正方向；然后，经过x轴上x2h处的 P2点进入磁场，并经过y轴上y2h处的P3点。不计重力。求,24.,（2）粒子到达P2时速度的大小和方向。,（3）磁感应强度的大小。,（l）电场强度的大小。,例4、如图所示，水平虚线上方有场强为E1的匀强电场，方向竖直向下，虚线下方有场强为E2的匀强电场，方向水平向右；在虚线上、下方均有磁感应强度相同的匀强磁场，方向垂直纸面向外。ab是一长为L的绝缘细杆，竖直位于虚线上

20、方，b端恰在虚线上。将一套在杆上的带电小环从a端由静止开始释放，小环先加速而后匀速到达b端，环与杆之间的动摩擦因数v=0.3,环的重力不计,当环脱离杆后在虚线下方沿原方向作匀速直线运动,求：(1)E1与E2的比值。(2)若撤去虚线下方的电场,小环进入虚线下方后的运动轨迹为半圆,圆周半径为,环从a到b的过程中克服摩擦力做功Wf与电场做功WE之比有多大。,1、速度选择器如图，在平行板电容器中，电场强度E和磁感应强度B相互垂直。具有某一速度v的带电粒子将沿虚线通过不发生偏转，而其它速度的带电粒子将发生偏转。这种器件能把上述速度为v的粒子选择出来，所以叫速度选择器。试证明带电粒子具有的速度v=E/B，

21、才能沿图示的虚线通过。,四、几种实际应用,2、霍尔效应如图，厚度为h，宽度为d的导体板放在垂直于它的磁感应强度为B的匀强磁场中，当电流通过导体时，在导体板的上侧面A和下侧面A之间会产生电势差，这种现象称为霍尔效应。实验表明，当磁场不太强时，电势差为U，电流I和B的关系为U=KIB/d。式中的比例系数K为霍尔系数。设电流I是电子的定向移动形成的，电子的平均定向速度为v，电量为e，回答以下问题：,（1）达到稳定状态时，导体板上侧面A的电势 下侧面A的电势（填“高于”、“低于”或“等于”）。,（2）电子所受洛伦兹力的大小为 。,（3）当导体板上下两侧之间的电势差为U时，电子所受静电力的大小为,（4）

22、证明霍尔系数为K=1/ne，其中n为导体单位体积中电子的个数。,、磁流体发电机（1）如图，一束等离子体射入两平行金属板之间的匀强磁场中，导线CD将受到力的作用，下列说法正确的是 （ ）A、等离子体从右方射入，CD受到向左的作用力B、等离子体从右方射入，CD受到向右的作用力C、等离子体从左方射入，CD受到向左的作用力D、等离子体从左方射入，CD受到向右的作用力,（2）实验用磁流体发电机，两极板间距d=20cm，磁场的磁感应强度B=5T，若接入额定功率P=100W的灯泡，正好正常发光，且灯泡正常发光时电阻R=100，不计发电机内阻，求：等离子体的流速为多大？若等离子体均为一价离子，每秒钟有多少个什

23、么性质的离子打在下极板？,、电磁流量计如图为电磁流量计的示意图，非磁性管直径为d，内有导电液体流动，在垂直液体流向的方向上加一指向纸里的匀强磁场，测得液体a、b两点间的电势差为U，则管内导电液体的流量Q= m3/s。,5、高能粒子在现代高科技活动中具有广泛应用，如微观粒子的研究、核能的生产等。粒子加速器是实现高能粒子的主要途径。如图所示为环形粒子加速器的示意图，图中实线所示环形区域内存在垂直纸面向外的大小可调节的匀强磁场，质量为m，电荷量为q的带正电的粒子在环中做半径为R的圆周运动。A、B为两块中心开有小孔的极板，原来电势都为零，每当粒子飞经A板时，A板电势升高为+U，B板的电势保持为零，粒子

24、在两板之间电场中加速，每当粒子离开B板时，A板电势又突然变为零，粒子在电场的一次次加速下动能不断增大 ，但绕行半径R却始终保持不变。,（1）设t=0时，粒子静止在A板小孔处，在电场作用下开始加速，并绕行第一圈。求粒子绕行n圈回到A板时获得的总动能Ek,（2）为使粒子始终保持在半径为R的圆轨道上运动，磁场必须周期性递增，求粒子绕行第n圈时，磁感应强度Bn应为多少？,（3）求粒子绕行n圈所需总时间（粒子通过A、B之间的时间不计）,（4）在粒子绕行的整个过程中，A板电势是否可始终保持+U？为什么？,回旋加速器,、质谱仪质谱仪是一种测定带电粒子质量和分析同位素的重要仪器，设从离子源S产生出来的离子初速度为零，经过电压为U的加速电场加速后，进入一平行板电容器C中，电场强度为E的电场和磁感应强度为B1的磁场相互垂直，具有某一速度的离子将沿如图所示的直线穿过两板间的空间而不发生偏转，再进入磁感应强度为B2的磁场，最后打在记录它的照相底片上的P点,（1）证明能穿过电容器C的离子具有的速度为v=E/B（2）若测得P点到入口处S1的距离为x，证明离子的质量为,