 第七章应力和应变分析课件.ppt
第七章应力和应变分析课件.ppt
《第七章应力和应变分析课件.ppt》由会员分享,可在线阅读,更多相关《第七章应力和应变分析课件.ppt(93页珍藏版)》请在三一办公上搜索。
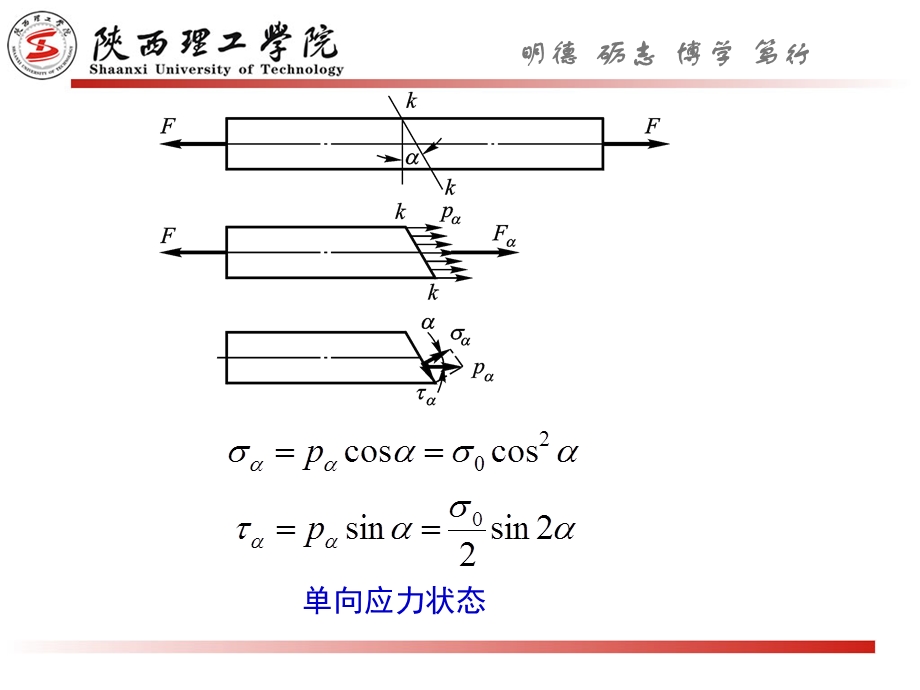
1、7-1 应力状态概述 7-2 二向和三向应力状态的实例 7-3 二向应力状态分析解析法 7-4 二向应力状态分析图解法 7-5 三向应力状态 7-8 广义胡克定律 7-9 复杂应力状态的应变能密度 7-10 强度理论概论 7-11 四种常用强度理论,第七章 应力和应变分析,7-1 应力状态概述,问题的提出: 为什么塑性材料拉伸时会出现滑移线? 为什么脆性材料扭转时沿45螺旋面断开?,单向应力状态,纯剪切应力状态,重 要 结 论,不仅横截面上存在应力,斜截面上也存在应力;不仅要研究横截面上的应力,而且也要研究斜截面上的应力。,过一点不同方向面上应力的集合,称之为这一点的应力状态。,应 力,指明,
2、应力表示单元体:,dx、dy、dz(微小的正六面体)单元体某斜截面上的应力就代表了构件内对应点同方位截面上的应力。,B、C单向受力,0,A纯剪切, 0,D既有 ,又有,主平面单元体的三个相互垂直的面上都无切应力。,主应力主平面上的正应力(也是单元体内各截面上正应力的极值)。,通过结构内一点总可找到三个相互垂直的截面皆为主平面。,对应的有三个主应力,相应的用 、 、 来表示,它们按代数值的大小顺序排列,即,7-2 二向和三向应力状态的实例,7-3 二向应力状态分析解析法,平面应力状态的普遍形式:在常见的受力构件中,在两对平面上既有正应力又有切应力。可将该单元体用平面图形来表示。,、正负号规定:拉
3、为正,压为负;以对微单元体内任意一点取矩为顺时针者为正,反之为负;,单元体各面上的已知应力分量 、 和 、 ,确定任一斜截面上的未知应力分量,从而确定该点处的主应力和主平面。,规定: 截面外法线同向为正; a绕研究对象顺时针转为正; 逆时针为正。,一、任意斜截面上的应力,设:斜截面面积为A,由分离体平衡得:,同理:,二、极值应力,max在剪应力相对的项限内,且偏向于x 及y大的一侧。,例 分析受扭构件的破坏规律。,解:确定危险点并画其原 始单元体,求极值应力,O,破坏分析,铸铁,例 图示应力状态(单位:Mpa),求:(1)斜截面上的应力;(2)主应力的大小;(3)主平面方位,并在单元体上绘出主
4、平面位置和主应力方向;(4)最大切应力。,解:(1)易知,,,(2)主应力大小,(3)主平面方位,法线与x轴夹角为67.5的主平面上对应的是2。,(4)最大切应力,7-4 二向应力状态分析图解法,对上述方程消去参数(2),得:,建立应力坐标系,如下图所示,(注意选好比例尺),二、应力圆的画法,在坐标系内画出点A( x,xy)和B(y,yx),AB与a 轴的交点C便是圆心。,以C为圆心,以AC为半径画圆应力圆;,三、单元体与应力圆的对应关系,四、在应力圆上标出极值应力,例 已知 求此单元体在30和 -40两斜截面上的应力。,例:讨论圆轴扭转时的应力状态,并分析铸铁件受扭转时的破坏现象。,解:1取
5、单元体ABCD,其中 , ,这是纯剪切应力状态。,2作应力圆 主应力为 ,并可确定主平面的法线。,3分析 纯剪切应力状态的两个主应力绝对值相等,但一为拉应力,另一为压应力。由于铸铁抗拉强度较低,圆截面铸铁构件扭转时构件将沿倾角为 45的螺旋面因拉伸而发生断裂破坏。,例 求图示单元体的主应力及主平面的位置。(单位:MPa),A,B,解:主应力坐标系如图,AB的垂直平分线与a 轴的交点C便是圆心,以C为圆心,以AC为半径画圆应力圆。, 1, 2,在坐标系内画出点,主应力及主平面如图,解法2解析法:分析建立坐标系如图,主单元体:六个平面都是主平面,若三个主应力已知,求任意斜截面上的应力:,7-5 三
6、向应力状态,这样,单元体上与主应力之一平行的各个斜截面上的正应力和剪应力,可由三个应力圆圆周上各点的坐标来表示。,至于与三个主方向都不平行的任意斜截面,弹性力学中已证明,其应力n和n可由图中阴影面内某点的坐标来表示。,在三向应力状态情况下:,max 作用在与2平行且与1和3的方向成45角的平面上,以1,3表示,例 :求图示应力状态的主应力和最大剪应力。(应力单位为MPa)。,解:,例 求图示应力状态的主应力和最大剪应力(应力单位为MPa)。,解:,例 试根据图a所示单元体各面上的应力作出应力圆,并求出主应力和最大切应力的值及它们的作用面方位。,(a),解: 1. 图a所示单元体上正应力z=20
7、 MPa的作用面(z截面)上无切应力,因而该正应力为主应力。,2. 与主平面z截面垂直的各截面上的应力与主应力z无关,故可画出显示与z截面垂直各截面上应力随截面方位角变化的应力圆。,(a),从圆上得出两个主应力46 MPa和-26 MPa。这样就得到了包括z=20 MPa在内的三个主应力。他们按代数值大小排序为 146 MPa, 220 MPa, 3-26 MPa。,(b),(a),3. 依据三个主应力值作出的三个应力圆如图b所示。,2a034可知为a017且由x截面逆时针转动,如图c中所示。,(c),(b),4. 最大切应力max由应力圆上点B的纵座标知为 max36 MPa,作用在由1 作
8、用面绕2 逆时针45 的面上(图c)。,(c),(b),7-8 广义胡克定律,一、单拉下的应力-应变关系,二、纯剪的应力-应变关系,三、复杂状态下的应力 - 应变关系,依叠加原理,得:,sz,sy,sx,当单元体三个平面皆为主平面时,,分别为 x , y , z 方向的主应变,与主应力的方向一致, ,三主平面内的切应变等于零。,对平面应力状态,2. 各向同性材料的体积应变,体积应变:每单位体积的体积变化,用表示,设单元体的三对平面均为主平面,其三个边长分别为 dx , dy , dz ,变形前体积:,变形后体积:,则体积应变为:.,代入广义胡克定律得:,即:任一点处的体积应变与该点处的三个主应


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 第七 应力 应变 分析 课件
 三一办公所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三一办公所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。




链接地址:https://www.31ppt.com/p-1838483.html