 大学物理第8章机械波ppt课件.ppt
大学物理第8章机械波ppt课件.ppt
《大学物理第8章机械波ppt课件.ppt》由会员分享,可在线阅读,更多相关《大学物理第8章机械波ppt课件.ppt(68页珍藏版)》请在三一办公上搜索。
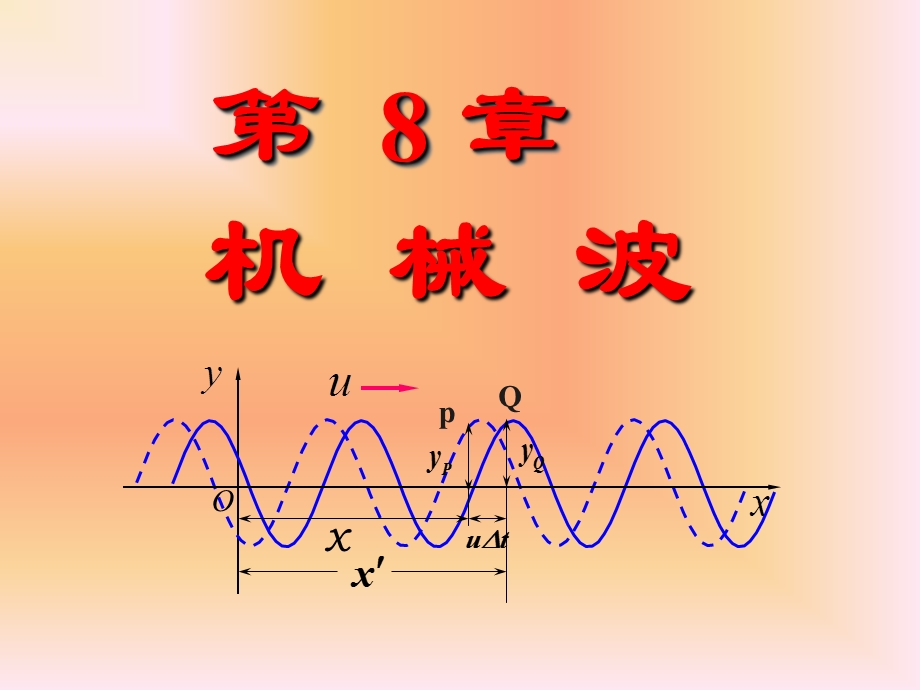
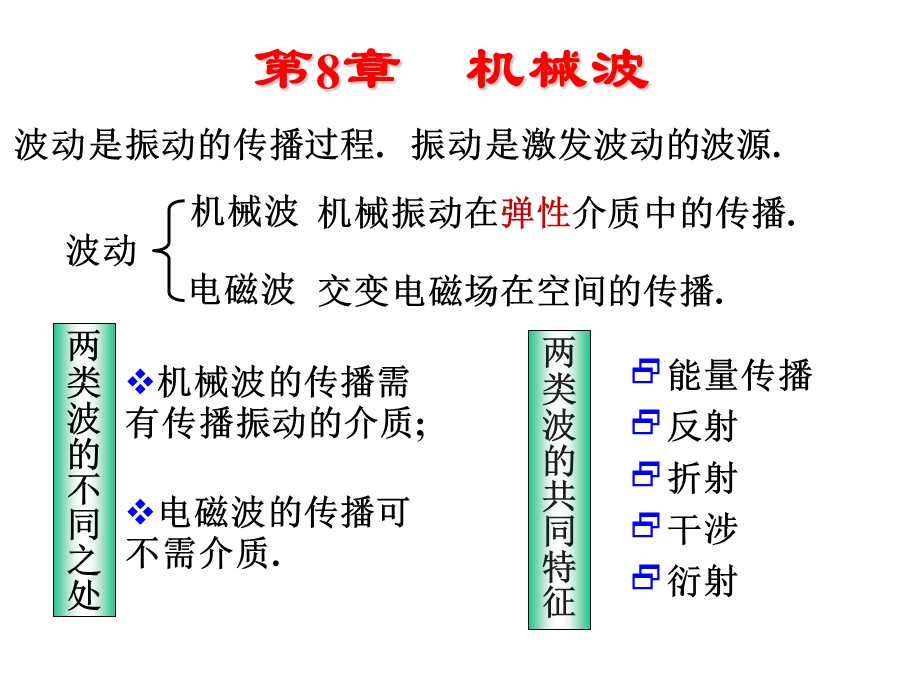
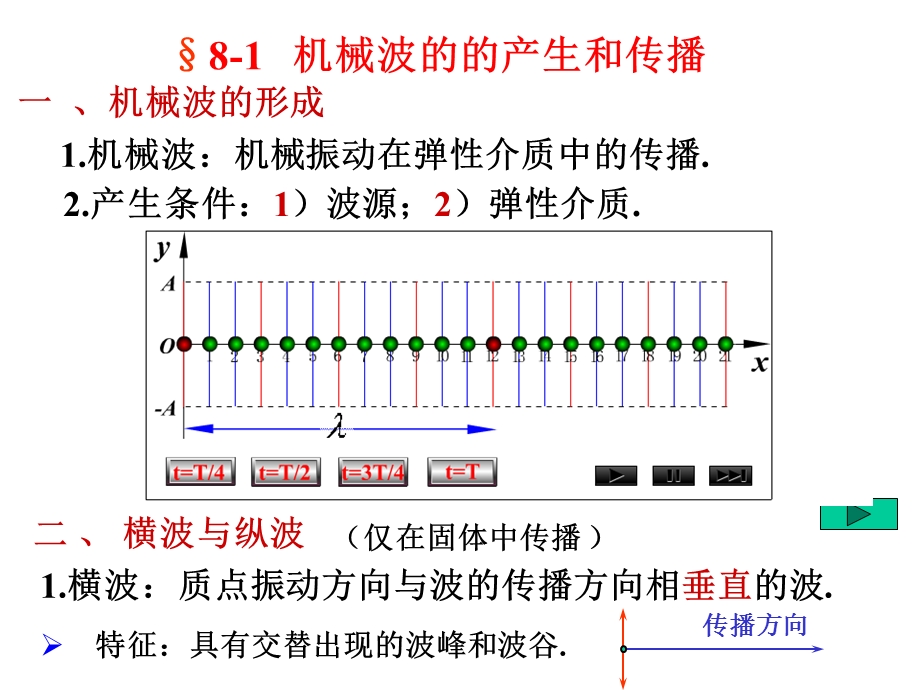
1、第 8 章,机 械 波,O,p,Q,x,两类波的不同之处,机械波的传播需有传播振动的介质;,电磁波的传播可不需介质.,能量传播反射折射干涉衍射,两类波的共同特征,第8章 机械波,一 、机械波的形成,2.产生条件:1)波源;2)弹性介质.,1.机械波:机械振动在弹性介质中的传播.,8-1 机械波的的产生和传播,1.横波:质点振动方向与波的传播方向相垂直的波.,(仅在固体中传播 ),二 、 横波与纵波,特征:具有交替出现的波峰和波谷.,2.纵波:质点振动方向与波的传播方向互相平行的波.,(可在固体、液体和气体中传播),特征:具有交替出现的密部和疏部.,介质中各质点只在各自的平衡位置附近振动,介质中
2、各质点的振动频率相同,但相位不同。即:沿波的传播方向上各质点作相似、相位依次落后的振动。-波是振动状态的传播。,振动是描写一个质点振动。,波动是描写一系列质点在作振动。,传播方向,判断质点振动方向,振动与波动的区别,三 、 描写波动过程的物理量,1. 波长 :沿波的传播方向,两个相邻的、相位差为 的振动质点之间的距离,即一个完整波形的长度.,波形图,2. 周期 :波前进一个波长的距离所需要的时间.,频率 :周期的倒数. 即单位时间内波动所传播的完整波的数目.,3. 波速 :波动过程中,某一振动状态(即振动 相位)单位时间内所传播的距离(相速).,即:周期或频率与介质无关,四 、 波的几何描述,
3、波线:表示波的传播方向的射线(波射线),波面:媒质振动相位相同的点组成的面(同相面),波前:某时刻波到达的各点所构成的面(波阵面),球面波平面波在各向同性均匀介质中,波线与波阵面垂直.,简谐波:,一 、波函数:,各质点相对平衡位置的位移,波动是集体表现,各质点在同一时刻的振动位移是不同的。,波线上各质点平衡位置,8-2.平面简谐波的波函数,任意时刻任意位置处的质点的振动位移为波函数。,简谐振动在弹性介质中的传播。,表示波动的数学表达式-波动方程,1.设原点处质点的振动方程,2.求x 处质点的振动方程,P 点的振动比原点落后一段时间,P点的振动方程,因为 P点为任意点,所以波函数为,推导波函数,
4、3.波沿X 轴正向传播时的波函数:,x处质点比原点处质点振动滞后的相位,x处质 点比原点振动落后的时间(波从原点传到x点所需时间,x处质点振动的初相位。,振动的角频率。,x/u :,x /u =2x/:,各量的物理意义,:,原点处质点振动的初相位, :,- x/u + = -2x/ + :,4.波沿X 轴负向传播时的波函数:,1)给出下列波函数所表示的波的传播方向和x=0 的初相位.,2)平面简谐波的波函数为 , 式中A,B,C 为正常数,求波长、周期及波速.,(向 x 轴正向传播, j= ),(向 x 轴负向传播, j= ),例1:波源振动方程为,波速,求:波函数;,波长、频率;,解:,波源
5、,波函数, x=5m处P质点的振动与波源的相位差。,.波长、频率,P 点落后反映在相位上为 20 , 即振源完成 10 个全振动后,P 点开始振动。,沿x正方向传播。,例2:如图有一平面简谐波在空间传播,已知P点的振动方程为,(1)分别就图中的两种坐标写出其波动方程(2)写出距P点为b的Q点的振动方程,任意点x滞后P点振动的相位差,波动方程,原点的振动方程,波动方程,(2)写出距P点为b的Q点的振动方程,将,注意:波动方程与原点有关,振动方程与原点无关。,将,二、波函数的物理意义,1.当x固定时,波函数为,波线上各点的简谐运动图,并给出该点与点 O 振动的相位差.,表示该点的简谐运动方程,,2
6、. 当t 一定时,波函数为,同一时刻,x1, x2两点的相位不同,表示该时刻波线上各点相对其平衡位置的位移,即此刻的波形.,3. 若 x, t 均变化,波函数表示波形沿传播方向的运动情况(行波).,设t时刻位于质点P点的位移为:,经过t时刻后, Q 点的位移:,t 时刻P点的运动状态经t 时间传到了Q点,所以波函数表示波形的传播过程。当t连续变化时,波形连续不断前进,故波动过程可以表示为波形随时间不断向前移动的过程,波形不断前进的波称行波。,三、应用波函数求解的问题,1.已知原点的振动方程,,波动方程,2.已知p点的振动方程,,波动方程,3.已知波函数,求p点的振动方程,例3:如图(a)为t=
7、0时的波形曲线,经0.5s后波形变为(b)求(1)波动方程 (2)P点的振动方程,解:由图得,A=0.1 = 4m,(2) P点的振动方程,x=1,-0.1,O,波动方程, = /2,由图得O点的初相位为:,解:可由0 点在t=T/2时刻的状态求0 的初位相。,例4:已知一平面简谐波沿X轴正向传播,波速u=8m/s,在t= T/2 时刻波形图如下,求该波的波函数。,例5:一沿X轴正向传播的平面简谐波,在某一时刻的波形图如下图,求波长=?(SI制),解:分析 O 、p两点状态已知,则可由Op 两点的位相 求出波长,P点 t 时刻的相位,O点 t 时刻的相位,O , P 两点 的相位差,例6:如图
8、简谐波以余弦函数表示,求 O、a、b、c 各点振动初相位.,用旋转矢量分析,a点,b点,C点,例7:已知:一个向右传播的波在 x = 0点的振动曲线如图所示。试画出该波在t = 0 时的波形曲线。,解:,例8:一平面简谐波沿x正方向传播,振幅A10cm,圆频率 当t=1.0s时,位于x=10cm处的质点a经过平衡位置向y轴负方向运动。此时,位于x=20cm处的质点b的位移为5cm, 且向y轴正方向运动。设该波波长 ,试求该波的波动方程。,解:设该波的波动方程为:,求解的关键是求出波速u 及原点的初位相,方法:解析法。,所以,-(1),由题意知 t =1.0s时,解(1),(2)得,故得波动方程
9、为,得,注意b 点落后于a点,故同一时刻(t=1.0s) a点的位相取/2时,b点的位相只能取-/3 (不取5/3,还考虑了 10 cm 以及 xb-xa=10cm的条件。),同理,-(1),-(2),取,1.波动的动能,弹性介质中取一体积元 dV,质量,波函数,质元振动速度,8-3.波的能量,一、波的动能、势能和能量,动能,2.波动的势能,由于介质发生形变而具有势能,势能,3.波动的能量,在波的传播过程中,任意时刻的动能和势能不仅大小相等而且相位相同,同时达到最大,同时等于零。,1) 在波传动过程中,任意体积元的能量不守恒。,2) 对于某一体元,它的能量从零达到最大,这是能量的输入过程,然后
10、又从最大减到零,这是能量输出的过程,周而复始。-波是能量传播的一种形式。,4.波动的能量与振动能量的区别,振动能量中Ek、EP相互交换,系统总机械能守恒。,波动动能量中Ek、EP同时达到最大,同时为零,总能量随时间周期变化。,振动,极小,能量极大,波动,5.能量密度:,介质中单位体积内的波动能量。,6.平均能量密度,二、能流、波强,能流:单位时间内垂直通过介质中某一面积的能量称为,平均能流(波的功率) : 在一个周期内能流的平均值。,能流密度(波的强度):,单位:Js-1m-2 ,,W m-2,单位:Js-1,W,通过垂直于波动传播方向的单位 面积的平均能流。,声波频率 20 20000Hz,
11、超声波频率 20000Hz,次声波频率 20Hz,声波:,1.声波的频率范围,弹性介质中传播的机械纵波统称为声波,2.声强,声波的平均能流密度叫声强。,单位:W/m2,标准声强:, 的数量级为102 Hz时,标准声强振幅10 -10 m,(在1000Hz下,这个声强人能够勉强听到),三、声波、超声波、次声波,3.声强级,由于引起人的听觉声强范围是 10-1210-2 W/m2,相差较大。,声强级,单位:分贝,dB,正常说话60dB,,噪声70dB,,炮声120dB。,4.次声波,地震、火山爆发、原子弹爆炸等都会产生次声波。,根据次声波能量可测出爆炸的当量级。,次声波可在地表传播很远距离。,次声
12、武器。, 20Hz,一、波动中的几个概念,1.波线:,波的传播方向为波线。,2.波面,振动相位相同的各点组成的曲面。,3.波前,某一时刻波动所达到最前方的各点所连成的曲面。,平面波,球面波,8-4.惠更斯原理与波的衍射反射折射,1 .原理:介质中波动传播到的各点都可以看作是发射子波的波源,而在其后的任意时刻,这些子波的包络就是新的波前.,ut,t,t+t,t+t,t,平面波,球面波,二、惠更斯原理,2.应用:任何波在介质中的传播都可以根据该原理利用几何作图法由某一时刻的波前来确定下一时刻的波前,从而可确定波的传播方向。,3. 不足: 只能定性地说明。,1. 现象:波在传播过程中,遇到障碍物时其
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 大学物理 机械波 ppt 课件
 三一办公所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三一办公所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。




链接地址:https://www.31ppt.com/p-1695011.html